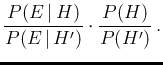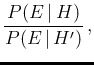We are finally at the core of the problem. Let Gauss speak:
“For, evidently, those systems will be regarded as the more probable
in which the greater expectation had existed of the event
which actually occurred.
The estimation of this probability rests upon the following theorem:
If, any hypothesis H being made, the probability of any
determinate event E is h, and if, another hypothesis H' being made excluding
the former and equally probable in itself, the probability of the same
event is h': then I say, when the event E has actually occurred,
that the probability that H was the true hypothesis, is to the
probability that H' was the true hypothesis, as h to h'.”
(Italic original, also put in evidence in the text as a quote
- see Fig. 1.)
Figure:
Extract of Theoria motus corporum...[7]
in which Gauss enunciates his theorem on how to
update probability ratios of incompatible hypotheses in the
light of an experimental observation. Note “tum dico” (“than I say”).
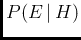 |
In modern notation:
There are no doubts that Gauss presents this result as
original (“then I say”, in Latin tum dico), although
it might be curious that it did not refer to results by Laplace,
who had been writing on probabilities of causes more than
thirty years before12 [10].
(For comparison, a few pages later, in article 177, Gauss
acknowledges Laplace
for having calculated the integral needed to normalize the `Gaussian'
distribution.) It is also curious the fact that Gauss starts saying
that “evidently, those systems will be regarded as the more probable
in which the greater expectation had existed of the event
which actually occurred”, considering
thus “evident”
what is presently known as `maximum likelihood principle',
but then taking care of proving it as a theorem (under
the well stated assumption of initially equally probable hypotheses).
The reasoning upon which the theorem is proved
is based on an inventory of equiprobable cases. This might seems
to limit the application to
situations in which this inventory is in practice feasible, like
in games of cards and of dice. Instead, this was the
way of reasoning of those times
to partition the space of possibilities, as it is clear from
the use that Gauss makes of his result, certainly not limited
to simple games.
Figure:
Partition of the space of possibilities
as it appears in the original work of Gauss [7].
The English translations of the three columns are [8]:
“that among them may be found”;
“in which should be assumed the hypothesis”; “in such a mode
as would give occasion to the event”. Then:
“ab 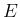 diuersus”
diuersus” 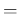 “different from
“different from 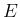 ”;
“ab
”;
“ab 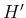 et
et 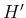 diuersa”
diuersa” 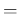 “different from
“different from 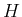 and
and 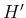 ”.
”.
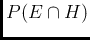 |
Figure 2 shows the original version of such a partition.
The six numbers of the first column, normalized to their sum, provide
the following probabilities:
The probabilities which enter the proof are those
of the 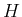 and
and 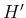
and those of the event 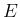 given
either hypothesis:
given
either hypothesis:
The probability of 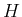 is modified by the observation of
is modified by the observation of 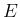 observing that, with
reference to Eqs. (10) and (11),
observing that, with
reference to Eqs. (10) and (11),
“after the event is known, when the cases 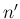 ,
, 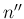 ,
, 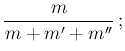 disappear
from the number of possible cases, the probabilities of the
same hypothesis will be
disappear
from the number of possible cases, the probabilities of the
same hypothesis will be
in the same way the probability of the
hypothesis 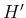 before and after the event,
respectively, will be expressed by
before and after the event,
respectively, will be expressed by
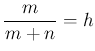 and
and
since, therefore, the same probability is assumed for the hypotheses
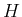 and
and 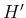 before the event is known, we shall have
before the event is known, we shall have
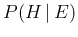 (G2)
(G2)
hence the truth of the theorem is readily inferred.”
That is, in our notation,
from which
Using then Eqs. (12) and (13),
yielding
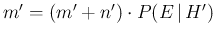 and
and
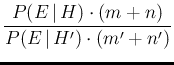 , we obtain
, we obtain
Applying finally the condition (G2), theorem (9)
is proved.
In reality, it is easy to see that,
being
Eq. (14)
contains the most general case
But Gauss contented himself with the sub-case of initially
probable hypotheses.
Why? The reason is most likely that he focused on the
inference
of the unknown values of the physical quantities of interest,
that he assumed a priori equally likely,
a very reasonable assumption for this kind of inferences,
if we compare the prior knowledge
with the information provided by observations
(see e.g. Ref. [9]).
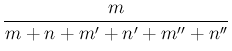
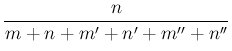
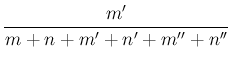
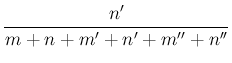
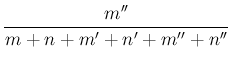
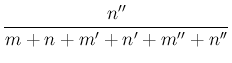
,
,
disappear from the number of possible cases, the probabilities of the same hypothesis will be
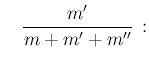
before and after the event, respectively, will be expressed by
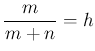 and
andand
before the event is known, we shall have
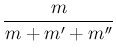
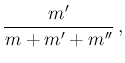
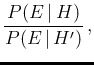
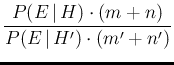 , we obtain
, we obtain