


Next: Why not to use
Up: P-value analysis of the
Previous: P-value based on the
P-value based on the argument that the highest excess could have shown up
everywhere in the time distribution
Again, the previous procedure can be easily criticized,
because ``the bin to which the test has been applied has been chosen
after having observed the data, while a peak would have been arisen,
a priori, everywhere in the plot.'' The standard procedure to overcome
this criticism is to calculate the probability that a peak of
that or higher value would have shown up everywhere in the data, i.e.
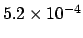 |
(3) |
where 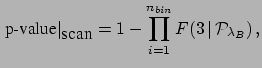 is the number of bins and
is the number of bins and 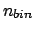 stands for the cumulative
distribution (the product in Eq. (3)
is based on the assumption of independence of the bins).
In our case we
get 13% or 23% depending whether a constant or varying background
is assumed, i.e. p-values above any over-optimistic choice of the p-value threshold.
stands for the cumulative
distribution (the product in Eq. (3)
is based on the assumption of independence of the bins).
In our case we
get 13% or 23% depending whether a constant or varying background
is assumed, i.e. p-values above any over-optimistic choice of the p-value threshold.
It is interesting to note that the 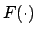 p-value can be reobtained
approximately as
p-value can be reobtained
approximately as
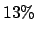 , showing
that even a very pronounced excess can be considered not significant if
a large number of observational
bins are involved in the experiment (and practitioners restrict arbitrary
the region to which the test is applied, if they want the test to state
what they would like...). The dependence of the result of the method
on observations far from the
region where there could be a good physical reason to have a signal is
annoying (and for this reason, practitioners who choose
a suitable region around the peak do, intuitively, something correct...).
On the other hand, the reasoning does not take into account that other
bins could be interested by the signal.
, showing
that even a very pronounced excess can be considered not significant if
a large number of observational
bins are involved in the experiment (and practitioners restrict arbitrary
the region to which the test is applied, if they want the test to state
what they would like...). The dependence of the result of the method
on observations far from the
region where there could be a good physical reason to have a signal is
annoying (and for this reason, practitioners who choose
a suitable region around the peak do, intuitively, something correct...).
On the other hand, the reasoning does not take into account that other
bins could be interested by the signal.
We shall see in Sec. 4.3 how to
use properly the prior knowledge that a (physically motivated)
signal could have appeared everywhere in the histogram.



Next: Why not to use
Up: P-value analysis of the
Previous: P-value based on the
Giulio D'Agostini
2005-01-09
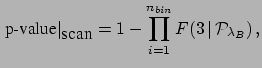 is the number of bins and
is the number of bins and ![]() p-value can be reobtained
approximately as
p-value can be reobtained
approximately as
![]() , showing
that even a very pronounced excess can be considered not significant if
a large number of observational
bins are involved in the experiment (and practitioners restrict arbitrary
the region to which the test is applied, if they want the test to state
what they would like...). The dependence of the result of the method
on observations far from the
region where there could be a good physical reason to have a signal is
annoying (and for this reason, practitioners who choose
a suitable region around the peak do, intuitively, something correct...).
On the other hand, the reasoning does not take into account that other
bins could be interested by the signal.
, showing
that even a very pronounced excess can be considered not significant if
a large number of observational
bins are involved in the experiment (and practitioners restrict arbitrary
the region to which the test is applied, if they want the test to state
what they would like...). The dependence of the result of the method
on observations far from the
region where there could be a good physical reason to have a signal is
annoying (and for this reason, practitioners who choose
a suitable region around the peak do, intuitively, something correct...).
On the other hand, the reasoning does not take into account that other
bins could be interested by the signal.