


Next: About the naturalness of
Up: Conclusions and discussion
Previous: About the choice of
About the choice of the quarter of the meridian
It is clear that, once
the académiciens were bound to the decimal system, decided by the
first commission, and the unit of length had to be related to Earth
dimensions, the unit of length of practical use had to be
a small decimal sub-multiple of an Earth dimension.
But why the quarter of the meridian, instead of the meridian itself?
The Rapport [2] does not give any
justification of the choice,
as if all other possibilities were out of question.
And this is a bit strange. The meridian as unit of length
had no tradition at all, and there had been no discussion
about which submultiple to use.
Evidence against the naturalness of the
quarter of meridian seems to us provided
by the fact that the
vulgarization of the definition of the meter, as it is often
taught at school and as it is memorized by most people, is the
forty millionth part of `something', where this `something' is
often remembered as the `equator' or the `maximum circle'.
It could be that we have nowadays a different sensitivity to the subject
(we have made a little poll among
friends and colleagues, and our impression has been unanimously
confirmed), but we find
it hard to be rationally convinced by the arguments
of the following kind:
Once it has been chosen as base, will either the whole meridian
or a sensible part
of it be taken as a unit?
The wholeness? Out of question! The half, that stretches from one
pole to the other,
may not
be easily conceived by our mind because of the part which is located
``below'',
in the other hemisphere.
This is not the case of the quarter of
the meridian that, on the contrary,
can be easily imagined:
it stretches from ``one pole to the equator''.
In the future it will be said: France opened the divider and pointed
it on one pole and the equator,
a sentence that will be greatly successful.
There is another reason, that is really scientific and supports the meridian:
its quarter is the arc intersected by the right angle.
That's right: however, why should it be considered as a further advantage?
Simply because the right angle is considered as the natural angle,
the angle of the vertical and the gravity. It is the unit-angle,
the degree is nothing but its subdivision.
(Ref. [35], p. 55 of the Italian translation)
What would be the alternatives?
As an exercise, we show in table 5
some possible `natural' choices of units of length based on the
dimensions of Earth, together with a reasonable decimal
sub-multiple as practical unit.
Table:
Some possible choices of units of length based on the
dimensions of Earth, assumed to be spherical,
together with a reasonable decimal
sub-multiple as practical unit and the half period of the simple
pendulum of such practical unit. (Analogous quantities can be defined
assuming an ellipsoid).
| unit |
decimal |
practical unit |
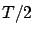 |
| |
sub-multiple |
(cm) |
(s) |
| radius |
1/10000000 |
64 |
0.803 |
| diameter |
1/10000000 |
128 |
1.135 |
| meridian |
1/100000000 |
40 |
0.635 |
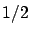 meridian (pole-pole) meridian (pole-pole) |
1/10000000 |
200 |
1.419 |
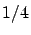 meridian (pole-equator) meridian (pole-equator) |
1/10000000 |
100 |
1.004 |
| 45th parallel |
1/100000000 |
28 |
0.534 |
| one radiant along the meridian |
1/10000000 |
64 |
0.803 |
| (same as radius) |
|
|
|
| 1 degree of Earth's arc |
1/100000 |
111 |
1.057 |
1 minute of Earth's arc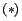 |
1/1000 |
185 |
1.367 |
| 1 second of Earth's arc |
1/100 |
31 |
0.558 |
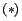 Equal to 1 nautical mile,
that is 1852m. Equal to 1 nautical mile,
that is 1852m. |
Sub-multiples of the length of the meridian, e.g. one part
over 10000000 or one part over 100000000, had led to a `meter' of
400 or 40 of `our' centimeters. The former is certainly too large,
but the latter is quite appropriate for daily use, and,
indeed, it falls in a range of length that is better perceived
by people (one of the criticisms to the meter is its unnaturality, at least
compared for example to the foot or even to the first standardized unit,
the cubit).
Even the pole-to-pole arc would have yield a better practical unit,
very close to the toise.
We see from table 5 that the
10000000 part of the quarter of meridian is the
closest to the length of the seconds pendulum.
So, when the French scientists proposed the new unit of length,
we think it is possible, among the many `defensible natural units',
they chose the closest to the seconds pendulum.
The reason could be a compromise with
the strenuous defenders of the seconds pendulum. Or it could have happened
that, since they had in mind some `cooperation' between
the new unit and ``a pendulum
having a determined length''[2], choosing a unit close
to the well studied seconds pendulum would have
simplified the intercalibrations.



Next: About the naturalness of
Up: Conclusions and discussion
Previous: About the choice of
Giulio D'Agostini
2005-01-25