


Next: The 1793 provisional meter
Up: Establishing the length of
Previous: Establishing the length of
Measuring the size of Earth had been a challenging problem
for ages, since it was first realized that
Earth is spherical, i.e.
at least by the sixth century B.C. [24].
The most famous ancient estimate is that due to Eratosthenes
(276-195B.C.), who reported a value of 250000 stadia,
i.e. about
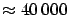 kilometers,
if we take 159m per stadium.29
kilometers,
if we take 159m per stadium.29
Table:
Some milestones in measuring the Earth meridian. 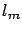 stands for the length of the meter calculated as the 40000000th
part of the meridian (for some important cases,
stands for the length of the meter calculated as the 40000000th
part of the meridian (for some important cases, 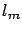 is
also given in lignes -- see
Table 1 for conversion).
In the results expressed in
the form `
is
also given in lignes -- see
Table 1 for conversion).
In the results expressed in
the form `
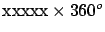 ' xxxxx stands for the
length of one degree meridian arc (
' xxxxx stands for the
length of one degree meridian arc (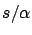 in the text).
Ancient estimates have to be taken
with large uncertainty (see e.g. Ref.[24]).
in the text).
Ancient estimates have to be taken
with large uncertainty (see e.g. Ref.[24]).
|
Author(s) |
Year |
Value |
Unit |
km value |
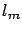 (m) (m) |
|
|
|
|
|
|
{lignes} |
|
Eratosthenes |
(III B.C.) |
250000 |
stadium
|
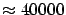 |
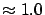 |
|
|
|
|
|
|
|
|
Caliph Al-Mamun |
820 |
56 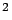 /3 /3 |
Arab mile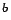 |
39986 |
0.9997 |
|
|
|
|
|
|
|
|
Fernel |
1525 |
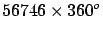 |
toise |
39816 |
0.9954 |
|
Snellius |
1617 |
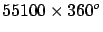 |
toise |
38661 |
0.9665 |
|
Norwood |
1635 |
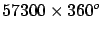 |
toise |
40204 |
1.0051 |
|
Picard |
1670 |
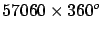 |
toise |
40036 |
1.0009 |
|
J. Cassini |
1718 |
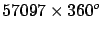 |
toise |
40062 |
1.0016 |
|
Lacaille and |
1740 |
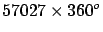 |
toise |
40013 |
1.00033 |
|
Cassini de Thury |
|
|
|
|
{443.44} |
|
|
|
|
|
|
|
|
[Lapland expedition |
1736 |
57438 360 360
|
toise |
40302 |
1.0075] |
|
[Peru expedition |
1745 |
56748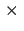 360 360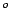
|
toise |
39817 |
0.9954]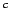 |
|
|
|
|
|
|
|
|
Delambre and |
1799 |
20522960 |
toise
|
40000 |
1 |
|
Méchain |
|
|
|
|
{443.296} |
|
|
|
[57019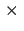 360 360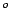 |
toise |
40008 |
1.00019 ]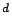 |
|
|
|
|
|
|
{443.38} |
|
|
|
|
|
|
|
|
present value |
|
40009152 |
m |
40009.152 |
1.000229 |
|
|
|
|
|
|
{443.3975} |
 Stadium estimated to be 159 m. Stadium estimated to be 159 m. |
 Arab mile estimated to be 1960 m [24]. Arab mile estimated to be 1960 m [24]. |
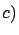 Values obtained at extreme latitudes, very
sensitive to Earth ellipticity. Values obtained at extreme latitudes, very
sensitive to Earth ellipticity. |
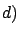 The entries of this line assume
a spherical model for Earth, as for older estimates. The entries of this line assume
a spherical model for Earth, as for older estimates. |
The value of 57019 toises per degree is obtained dividing
the 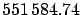 toises of the toises of the |
meridian arc Dunkerque-Barcelona by their
difference in latitude,
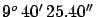 [35] . [35] . |
The principles of measurement of the Earth parameters,
exposed at an introductory level,
as well as milestones of these achievements, can be found
in Ref. [24]. The basic idea is rather
simple: if one is able to measure, or estimate somehow,
the length of an arc of meridian (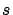 )
and its angular opening (
)
and its angular opening (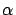 ),
the length of the meridian can be determined
as
),
the length of the meridian can be determined
as
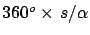 ,
if a circular
shape for the meridian is assumed (i.e. for a spherical Earth).
The angle
,
if a circular
shape for the meridian is assumed (i.e. for a spherical Earth).
The angle 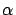 can be determined from astronomical observations.
The measurement of
can be determined from astronomical observations.
The measurement of 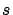 is bound to the technology of the epoch
and varies from counting the number of steps in the early days
to modern triangulation techniques [24].
Indeed, the rather accurate measurements between the
16th and 18th centuries
provided the results in terms of
is bound to the technology of the epoch
and varies from counting the number of steps in the early days
to modern triangulation techniques [24].
Indeed, the rather accurate measurements between the
16th and 18th centuries
provided the results in terms of 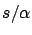 , expressed e.g. in toises/degree
(see Table 3).
, expressed e.g. in toises/degree
(see Table 3).
As we can see in Table 3, not exhaustive
of all the efforts to pin down the Earth dimensions,
there was quite
a convergence on the length of the unitary meridian arc in Europe,
as well as a general consistency with older measurements.
For example, taking the Lacaille and Cassini de Thury result,
based on the about 950 km arc of the Paris
meridian30 across all France,
it is possible to calculate a value of 443.44 lignes for the
new unit of measurements, assuming a spherical Earth
(
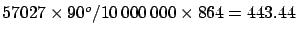 ). Even a conservative
estimate would give a value of 443.4 lignes, with an uncertainty
on the last digit -- a difference of three lignes (about 6 mm)
with respect to the length of the second pendulum. That was
definitely known to Borda and colleagues.
). Even a conservative
estimate would give a value of 443.4 lignes, with an uncertainty
on the last digit -- a difference of three lignes (about 6 mm)
with respect to the length of the second pendulum. That was
definitely known to Borda and colleagues.
However, apart from experimental errors in the determination
of the 57027 toise/degree, the value of 443.44
was still affected by uncertainties
due to the shape of Earth. At that time the scientists were
rather confident on an elliptical shape of the meridians,
resulting from the Earth flattening at the poles. In fact,
centrifugal acceleration due to rotation is responsible for the bulge
of the Earth at the equator. The resulting Earth shape is
such that the total force (gravitational plus centrifugal)
acting on a body at the Earth surface
is always orthogonal to the `average' surface of the Earth.
If that were not the case, there would be tangential forces
that tended to push floating masses towards the equator,
as eloquently stated by Newton: ``...if our Earth were not a little higher around the equator
than at the poles, the seas would subside at the poles and,
by ascending in the region of the equator, would flood everything there.''
(Cited in Ref. [33].)
Newton had estimated an Earth ellipticity of 1/229[34].
Several measurements had been done during the 18th century
to determine the value of Earth flattening.
In particular, there had been an enormous
effort of the French Academy of Sciences, that supported
measurements in France as well as expeditions at extreme
latitudes, up to the arctic
circle and down to the equator.31
The latter measurements were essential in order
to gain sensitivity on the flattening effect. In fact, the
unitary arc length 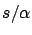 gives the local curvature
along the meridian around the region of the measurements.
As a consequence,
gives the local curvature
along the meridian around the region of the measurements.
As a consequence,
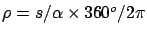 is equal to the radius of the circle that approximates locally
the meridian ellipse.
is equal to the radius of the circle that approximates locally
the meridian ellipse.
Figure:
An exaggerated representation of the ellipsoidal
Earth shape, showing local circles at the equator and
at the pole (the ellipse is characterized by
the semi-axes 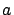 and
and 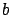 ).
The ellipse of the figure has a flattening of about 1/2,
i.e. an eccentricity of 0.87.
(A flattening of 1/298, corresponding to the
Earth one, i.e. a minor axis being 0.3% smaller
than the major axis, is imperceptible to the human eye.)
Note how the equatorial local
circle underestimates the ellipse circumference,
while the polar one overestimates it.
).
The ellipse of the figure has a flattening of about 1/2,
i.e. an eccentricity of 0.87.
(A flattening of 1/298, corresponding to the
Earth one, i.e. a minor axis being 0.3% smaller
than the major axis, is imperceptible to the human eye.)
Note how the equatorial local
circle underestimates the ellipse circumference,
while the polar one overestimates it.
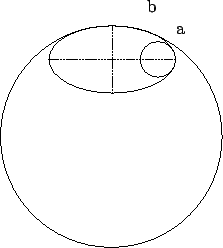 |
As it can be easily understood from figure 1,
the curvature decreases with the latitude: the radius of
the `local circle' is minimum at the equator and maximum at the pole.
The measurements of arcs of meridian at several
latitudes (two distant latitudes are in principle
sufficient) can yield the ellipse parameters.
Comparing the result of Lacaille-Cassini from Table 3
with the results of the Lapland and the Peru expeditions
from the same table, we see that 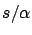 is indeed increasing with
the latitude (note these measurements were quite accurate --
for a very interesting account of the Peru expedition
see Ref. [37]). The combination of these and other
measurements gave values of the Earth flattening in the
range 1/280-1/310 [37], with a best estimate around
1/300, very close to the present value of 1/298
(see Table 4).
is indeed increasing with
the latitude (note these measurements were quite accurate --
for a very interesting account of the Peru expedition
see Ref. [37]). The combination of these and other
measurements gave values of the Earth flattening in the
range 1/280-1/310 [37], with a best estimate around
1/300, very close to the present value of 1/298
(see Table 4).
Table:
Earth data [38]. The geometrical data
refer to the WGS84 ellipsoid [37]. Note that the generic `radius of Earth'
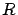 refers usually to the equatorial radius, but sometimes also
to the `average' equivolume radius.
In literature the name
`ellipticity' is often associated to what is called `geometric
flattening' in this table, and even to the difference of
equatorial and polar radii divided
by their average, i.e.
refers usually to the equatorial radius, but sometimes also
to the `average' equivolume radius.
In literature the name
`ellipticity' is often associated to what is called `geometric
flattening' in this table, and even to the difference of
equatorial and polar radii divided
by their average, i.e.
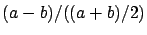 .
Anyway, the three different `ellipticities' give with good approximation
the same number, about
.
Anyway, the three different `ellipticities' give with good approximation
the same number, about 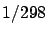 , because of the little deviation
of our planet from
a perfect sphere.
Note also that sometimes the flattening
is even confused with the ellipse eccentricity, that differs quite
a lot from flattening and ellipticity.
, because of the little deviation
of our planet from
a perfect sphere.
Note also that sometimes the flattening
is even confused with the ellipse eccentricity, that differs quite
a lot from flattening and ellipticity.
equatorial radius, 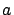 |
6378137m |
Polar radius, 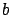 |
6356752m |
| Equivolume sphere radius |
6371000m |
Geometric flattening, 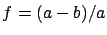 |
1/298.26 |
Ellipticity,
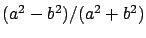 |
1/297.75 |
Eccentricity,
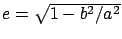 |
0.08182 = 1/12.2 |
(for 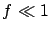 , , 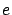 is about is about 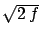 ) ) |
|
Mass, 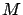 |
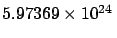 kg kg |
| Mean density |
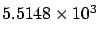 kgm kgm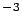 |
| Normal gravity at equator |
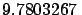 ms ms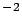 |
| Normal gravity at poles |
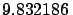 ms ms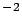 |
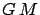 (where (where 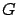 is the gravitational constant) is the gravitational constant) |
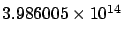 m m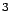 s s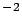 |
However, given such a tiny value of the flattening (imagine a soccer ball
squeezed by 0.7 mm), its effect on the circumference of
the ellipse is very small, of the order of a few parts
in 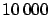 .
.
To summarize this subsection, we can safely state that
the length of the meridian, and hence
of any of its subdivisions, was known with a relatively high accuracy
decades before the
report that recommended the unit of length equal
to
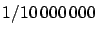 part of the quarter of meridian was produced.
In particular, for what this paper is concerned,
it was well known that the new standard
was equal to the length of the one seconds pendulum within
about half percent.
part of the quarter of meridian was produced.
In particular, for what this paper is concerned,
it was well known that the new standard
was equal to the length of the one seconds pendulum within
about half percent.



Next: The 1793 provisional meter
Up: Establishing the length of
Previous: Establishing the length of
Giulio D'Agostini
2005-01-25
