


Next: Partial combinations of results
Up: Partial results from ,
Previous:
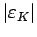
Since the third constraint depends on two strongly correlated
parameters, we need to consider a joint bivariate Gaussian distribution:
with
![$\mu_c=\mbox{E}[c]=3.4$](img79.png) ,
, 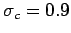 ,
,
![$\mu_d=\mbox{E}[d]=1.23$](img81.png) ,
, 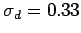 , and
, and
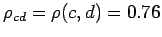 .
The integral
.
The integral
![\begin{displaymath}
f(\bar {\rho},\bar{\eta}\,\vert\,C_3) = \int\!\!\!\!\int_{-\...
...+c\,(1-\bar {\rho})]-d\right) \,
f(c,d)\,\mbox{d}c\,\mbox{d}c
\end{displaymath}](img84.png) |
(15) |
can be still evaluated
analytically but we omit here the final formula, just
giving the 3-D plot of the
resulting p.d.f. normalized in the region of interest (Fig. 5).
Figure:
Probability density function of
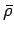 and
and 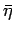 obtained by the constraint given by
obtained by the constraint given by
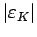 .
.
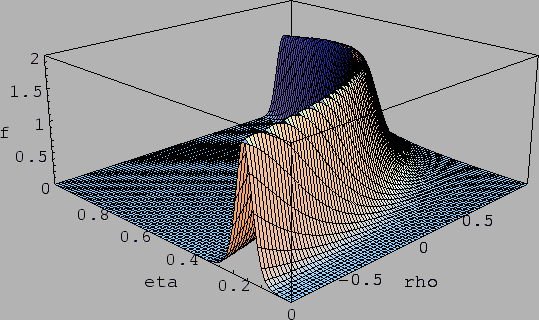 |
Giulio D'Agostini
2004-01-20
![\begin{displaymath}
f(\bar {\rho},\bar{\eta}\,\vert\,C_3) = \int\!\!\!\!\int_{-\...
...+c\,(1-\bar {\rho})]-d\right) \,
f(c,d)\,\mbox{d}c\,\mbox{d}c
\end{displaymath}](img84.png)