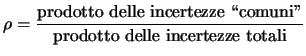Valutazione pratica di $\rho$ dovuto ad errori di calibrazione

Per ottenere in modo euristico una regoletta pratica per il calcolo del coefficiente di correlazione dovuto ad errori di calibrazione di zero o di scala si può ragionare nel seguente modo:

• per quanto detto precedentemente il coefficiente di correlazione è $\ge 0$;
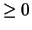• se lo strumento è perfettamente calibrato, non si introduce alcuna correlazione fra le misure e, nel contempo, è nullo il contributo all'incertezza totale;
• se l'incertezza dovuta alla calibrazione è molto maggiore di quella dovuta agli effetti casuali, essa domina l'incertezza globale e quindi la correlazione sarà di +1 (``100%'').

Il coefficiente di correlazione calcolato come

$$\rho = \frac{\mbox{prodotto delle incertezze \lq\lq comuni''}} {\mbox{prodotto delle incertezze totali}}$$

soddisfa questi requisiti (``comuni'' sta per ``introdotte dall'effetto sistematico comune''). In effetti, si può dimostrare che, per i casi che ci interessano, la formula è corretta.

Otteniamo quindi, per i due tipi di errori considerati:

errore di zero

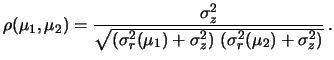$$\rho(\mu_1,\mu_2) = \frac{\sigma^2_z} {\sqrt{\left(\sigma_{r}^2(\mu_1)+\sigma^2_z\right)\, \left(\sigma_{r}^2(\mu_2)+\sigma^2_z\right)}}\,.$$ (36)

errore di scala

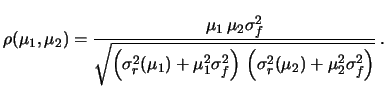$$\rho(\mu_1,\mu_2) = \frac{\mu_1\,\mu_2\sigma^2_f} {\sqrt{\left(\s... ..._1^2\sigma^2_f\right)\, \left(\sigma_{r}^2(\mu_2)+\mu_2^2\sigma^2_f\right)}}\,.$$ (37)