



Next: Raccomandazioni BIPM/ISO
Up: Coefficiente di correlazione
Previous: Valutazione pratica di dovuto
Indice
Le (36)
e (37)
permettono di calcolare i coefficienti
di correlazione e le covarianze fra grandezze misurate con lo
stesso strumento. Ma le correlazioni sono generate anche per altre
cause. Infatti, vale in generale:
più grandezze ottenute per misura indiretta
a partire da un insieme comune di grandezze di base, ciascuna nota con
una sua incertezza,
hanno in genere valori correlati.
Le grandezze misurate con lo stesso
strumento sono soltanto un caso particolare
in cui le stesse informazioni comuni sono le costanti di calibrazione.
Altri casi importanti sono:
- più grandezze misurate indirettamente da un insieme di grandezze
misurate direttamente;
- i parametri delle curve che descrivono una legge fisica
(ad esempio intercetta e coefficiente angolare di un fit lineare).
Per comodità diamo la regola generale di propagazione
che tiene conto delle correlazioni fra variabili di partenza
e fornisce anche le correlazioni fra le variabili di arrivo,
senza voler dare una
dimostrazione o giustificazione.
Per semplificare le formule usiamo la seguente notazione:
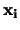
- sono le
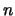 variabili di partenza (corrispondenti
alle
variabili di partenza (corrispondenti
alle 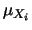 nel formalismo usato finora);
nel formalismo usato finora);
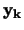
- sono le
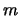 variabili di arrivo (corrispondenti
a
variabili di arrivo (corrispondenti
a 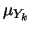 );
);
-
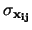 :
:
- è una notazione compatta che
riassume varianze e covarianze:
-
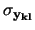
- sono le analoghe
delle
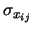 per le
per le 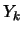 ;
;
-
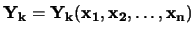
- sono le funzioni
che legano le
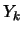 alle
alle 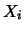 ;
;
- le derivate
- si intendono calcolate in corrispondenza
dei valori attesi (``migliori stime'') delle
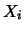 .
.
Con questa notazione
la formula compatta di propagazione di varianze e covarianze
è:
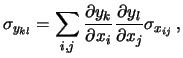 |
(38) |
dove la sommatoria si estende alle 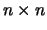 combinazioni degli indici
combinazioni degli indici 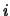 e
e 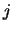 . Gli indici
. Gli indici 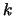 e
e 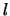 variano invece fra 1 e
variano invece fra 1 e 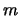 .
.
Come esempio, ricaviamo mediante la (38)
l'incertezza
della somma e della differenza
di due grandezze affette da errore di zero comune
facendo uso della (29) e
della (36).
Inoltre possiamo calcolare la covarianza fra 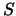 e
e 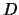 (e da questa, banalmente, il coefficiente di correlazione):
(e da questa, banalmente, il coefficiente di correlazione):
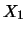 |
 |
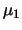 (vecchia notazione) (vecchia notazione) |
|
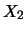 |
 |
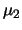 (vecchia notazione) (vecchia notazione) |
|
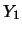 |
 |
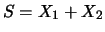 |
|
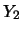 |
 |
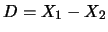 |
|
| |
|
|
|
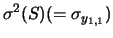 |
 |
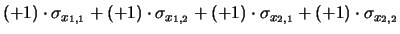 |
|
| |
 |
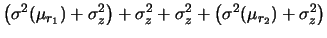 |
|
| |
 |
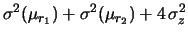 |
|
| |
|
|
|
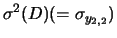 |
 |
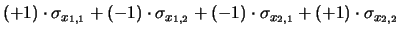 |
|
| |
 |
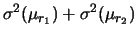 |
|
| |
|
|
|
Cov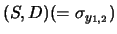 |
 |
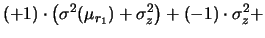 |
|
| |
|
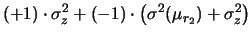 |
|
| |
 |
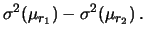 |
|
Abbiamo riottenuto 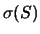 e
e 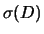 che conoscevamo
(vedi (27) e (28)).
che conoscevamo
(vedi (27) e (28)).
Per quanto riguarda la covarianza, si noti come
il risultato non sia affatto intuitivo.
Questo dovrebbe insegnare che,
quando i problemi diventano importanti e complicati, bisogna
fare molta attenzione agli effetti di correlazione.




Next: Raccomandazioni BIPM/ISO
Up: Coefficiente di correlazione
Previous: Valutazione pratica di dovuto
Indice
Giulio D'Agostini
2001-04-02
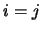 esse sono le
esse sono le 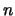 varianze delle
varianze delle 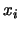 :
:
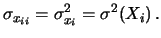
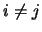 esse sono le covarianze:
esse sono le covarianze:
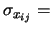 Cov
Cov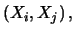
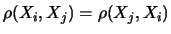 ,
ne segue che anche
Cov
,
ne segue che anche
Cov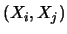 è uguale a
Cov
è uguale a
Cov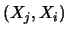 e quindi
e quindi
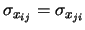 .
.
![]() e
e ![]() (e da questa, banalmente, il coefficiente di correlazione):
(e da questa, banalmente, il coefficiente di correlazione):