 |
Se la variabile può
verificarsi con sicurezza nell'intervallo
![]() ,
il valore atteso è
,
il valore atteso è ![]() e la deviazione standard vale
e la deviazione standard vale
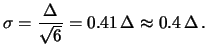 |
(50) |
C'è un'altra distribuzione triangolare che può avere
interessi pratici: il valore al quale si crede di più è ![]() e i gradi di fiducia decrescono linearmente verso gli estremi
e i gradi di fiducia decrescono linearmente verso gli estremi
![]() e
e ![]() , ma
, ma ![]() non corrisponde con il centro
dell'intervallo.
Chiamando
non corrisponde con il centro
dell'intervallo.
Chiamando
| (51) | |||
| (52) |
Quando
![]() , si riottengono
le formule del caso precedente. E' interessante
inoltre notare che, se la differenza fra
, si riottengono
le formule del caso precedente. E' interessante
inoltre notare che, se la differenza fra ![]() e
e ![]() è piccola si ottiene una deviazione standard
circa pari a quella ottenibile con un valore
intermedio fra i due:
è piccola si ottiene una deviazione standard
circa pari a quella ottenibile con un valore
intermedio fra i due:
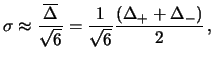
Un sottocaso particolare della triangolare asimmetrica
è quando
uno dei due ![]() è nullo ed il triangolo diventa rettangolo.
Questa distribuzione può modellizzare gradi di fiducia
che decrescono linearmente in un certo intervallo.
Ad esempio, ci possono essere delle ragioni
per ritenere che una grandezza definita non negativa
valga molto verosimilmente 0 e che comunque non
debba eccedere un certo valore
è nullo ed il triangolo diventa rettangolo.
Questa distribuzione può modellizzare gradi di fiducia
che decrescono linearmente in un certo intervallo.
Ad esempio, ci possono essere delle ragioni
per ritenere che una grandezza definita non negativa
valga molto verosimilmente 0 e che comunque non
debba eccedere un certo valore ![]() : si ottiene
una previsione di
: si ottiene
una previsione di
![]() .
.