Let us start reminding the well known
binomial and Poisson distributions, taken verbatim
from Ref. [13], just to introduce the notation
used in this note.
- Binomial distribution
-
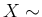 Binom
Binom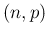 (hereafter “
(hereafter “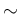 ” stands for “follows”);
Binom
” stands for “follows”);
Binom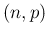 stands for binomial with parameters
stands for binomial with parameters
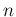 and
and 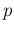 :
:
Expected value, standard deviation and variation coefficient
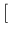
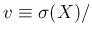 E
E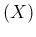
![$]$](img192.png) :
:
- Poisson distribution
-
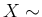 Poisson
Poisson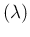 :
:
Expected value, standard deviation and variation coefficient
- Binomial
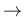 Poisson
Poisson
Binom![$\displaystyle (n,p)
\xrightarrow
[\begin{array}{l}n\rightarrow \infty \\
p\rightarrow 0 \\
(n\cdot p = \lambda)\end{array}]{}
{\mbox{Poisson}}(\lambda) \,.
$](img609.png)
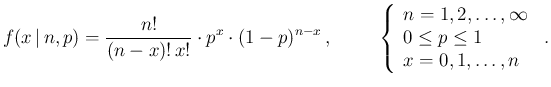
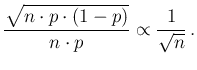
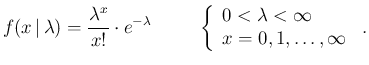
![$\displaystyle (n,p)
\xrightarrow
[\begin{array}{l}n\rightarrow \infty \\
p\rightarrow 0 \\
(n\cdot p = \lambda)\end{array}]{}
{\mbox{Poisson}}(\lambda) \,.
$](img609.png)