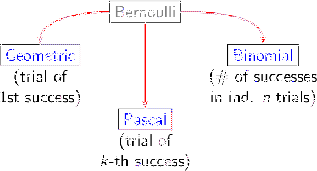
A Bernoulli process is characterized by
a probability 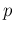 of success, to which
is associated the uncertain number
of success, to which
is associated the uncertain number 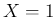 ,
and probability
,
and probability 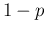 of failure,
to which is associated the uncertain number
of failure,
to which is associated the uncertain number 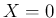 .
Therefore, technically, a Bernoulli distribution
is just a binomial with
.
Therefore, technically, a Bernoulli distribution
is just a binomial with 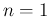 . But conceptually
it is very important, because it is the basic
process from which other distributions arise:
. But conceptually
it is very important, because it is the basic
process from which other distributions arise:
- a binomial distribution describes the probability
of the total number of
successes in
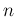 independent Bernoulli trials
`having' (or more precisely `believed to have')
the same probability of success
independent Bernoulli trials
`having' (or more precisely `believed to have')
the same probability of success 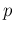 ;
;
- a geometric distribution describes the
probability (again assuming independence and constant
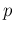 )
of the trial
at which36 the first success occurs;
)
of the trial
at which36 the first success occurs;
- a Pascal distribution (or negative binomial
distribution)
concerns finally the
trial at which the
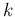 -th success occurs.37
-th success occurs.37