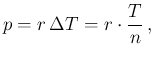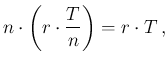A3. Poisson process

Let us now imagine phenomena that might happen at random at a given instant³⁸

$\epsfig{file=dago70.eps,clip=,width=0.55\linewidth}$

such that

the probability of one count in 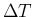$\Delta T$ is proportional to 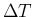$\Delta T$ , with 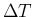$\Delta T$ `small', that is

$\displaystyle p=P($ “1 count in $\Delta T$ $\displaystyle '') = r\, \Delta T$
where the proportionality factor is interpreted as the intensity of the process;
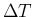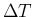the probability that two or more counts occur in $\Delta T$ is much smaller than the probability of one count (the condition holds if $\Delta T$ is small enough, that will be the case of interest):

$\displaystyle P(\ge 2\$ counts $\displaystyle ) \ll P(1\$ count $\displaystyle )\,;$
what happens in one interval does not depend on what happened (or `will happen') in other intervals (if disjoint).

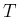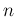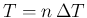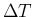Let us divide a finite time interval in small intervals, i.e. such that $T=n\,\Delta T$ . Considering the possible occurrence of a count in each small interval $\Delta T$ as an independent Bernoulli trial, of probability

$\displaystyle p=r\,\Delta T = r\cdot \frac{T}{n}\,,$

if we are interested in the total number of counts in T we get a binomial distribution, that is, indicating by 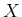the uncertain number of interest,

$\displaystyle X$

$\displaystyle \sim$

Binom $\displaystyle (n,p)\,.$

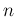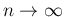But when is `very large' (` $n\rightarrow \infty$ ') we obtain a Poisson distribution with

$\displaystyle \lambda$

$\displaystyle =$

$\displaystyle n\cdot \left( r\cdot\frac{T}{n}\right) = r\cdot T\,,$

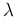equal to the intensity of the process times the finite time of observation. In particular, we can see that the physical quantity of interest is , while the Poisson parameter $\lambda$ is a kind of ancillary quantity, depending on the measurement time.