Fraction of sampled positives being really
infected or not
Putting all together, our rough expectation is that our sample
of 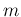 individuals will contain
individuals will contain
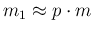 infected,
although we shall write it within this section
as an equality (`
infected,
although we shall write it within this section
as an equality (`
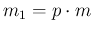 '),
and ditto for other related numbers.
Out of these
'),
and ditto for other related numbers.
Out of these 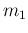 infected,
infected,
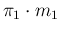 will be tagged as positive and
will be tagged as positive and
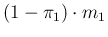 as negative.
Of the remaining
as negative.
Of the remaining
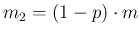 , not infected,
, not infected,
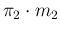 will be tagged as positive and
will be tagged as positive and
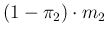 as negative. In sum, the expected numbers of
positive and negative will be
as negative. In sum, the expected numbers of
positive and negative will be
which we can rewrite as
So, just to fix the ideas with a numerical example
and sticking to
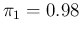 and
and
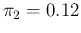 of Ref. [16],
in the case we sample 10000 individuals
we get, assuming 10% infected (
of Ref. [16],
in the case we sample 10000 individuals
we get, assuming 10% infected (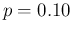 ),
),
- number of infected in the sample: 1000
(and hence 9000 not infected);
- infected tagged as positive: 980;
- infected tagged as negative: 20;
- not infected tagged as positive: 1080;
- not infected tagged as negative: 7920;
- total number of positive: 2060;
- total number of negative: 7940;
- fraction of the positives really infected:
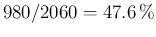 .
.