An old Problem in the Doctrine of Chances
Evaluating the probability of future events on the basis
of the outcomes of previous trials on `apparently the same conditions'
is an old, classical problem
in probability theory that goes back to about 250 years ago
and it is associated to the names of Bayes [21] and
Laplace [22]. The problem can be sketched
as considering events whose probability of occurrence depends
on a parameter which we generically indicate as 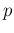 , i.e.
, i.e.
Idealized examples of the kind are the
proportion of white balls in a box containing a large number
of white and black balls (with the extracted ball
put back into the box after each extraction),
the bias of a coin and the ratio of the chosen
surface in which a ball thrown `at random' can stop,
with respect to the total surface of a horizontal table
(this was the case of the Bayes' `billiard', although the
Reverend did not mention a billiard).
A related problem concerns the number of times
(`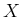 ') events of a given kind
occur in
') events of a given kind
occur in 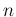 trials, assuming that
trials, assuming that 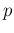 remains constant. The result is given by the
well known binomial, that is
remains constant. The result is given by the
well known binomial, that is
whose graphical causal model is shown in the left
diagram of Fig. ![[*]](crossref.png) .
.
Figure:
Graphical models of the binomial
distribution (left) and its `inverse problem'. The symbol
`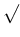 ' indicates the `observed' nodes
of the network, that is the value of the quantity
associated to it
is (assumed to be) certain. The other node
(only one in this simple case)
is `unobserved' and it is associated to
a quantity whose value is uncertain.
' indicates the `observed' nodes
of the network, that is the value of the quantity
associated to it
is (assumed to be) certain. The other node
(only one in this simple case)
is `unobserved' and it is associated to
a quantity whose value is uncertain.
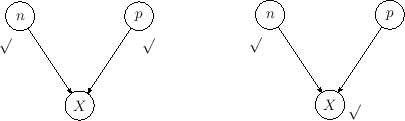 |
The problem first tackled in quantitative terms by Bayes and Laplace
was how to evaluate the probability of a `future' event 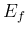 ,
based on the information that in the past
,
based on the information that in the past 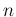 trials
the event of that kind occurred
trials
the event of that kind occurred 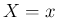 times (`number of successes')
and on the assumption of a regular flow from past
to future,11
that is assuming
times (`number of successes')
and on the assumption of a regular flow from past
to future,11
that is assuming 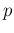 constant although uncertain. In symbols,
we are interested in
constant although uncertain. In symbols,
we are interested in
where 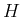 stands, as above, for all underlying
hypotheses. Both Bayes and Laplace realized that
the problem goes through two steps: first finding the probability
distribution of
stands, as above, for all underlying
hypotheses. Both Bayes and Laplace realized that
the problem goes through two steps: first finding the probability
distribution of 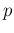 and then evaluating
and then evaluating
 taking into
account all possible values of
taking into
account all possible values of 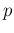 . In modern terms
. In modern terms
The basic reasoning behind these two steps
is expressly outlined in the Sixth and
Seventh Principle of the Calculus of Probabilities, expounded by
Laplace in Chapter III of his
Philosophical Essay on Probabilities [23]:
- the Sixth Principle, in terms of the possible causes
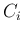 responsible of the observed event
responsible of the observed event 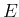 , is essentially
what is presently known as
Bayes' theorem, that is
, is essentially
what is presently known as
Bayes' theorem, that is
in which 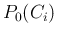 is the so called prior probability of
is the so called prior probability of 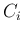 ,
i.e. not taking into account the piece of information
provided by the observation of
,
i.e. not taking into account the piece of information
provided by the observation of 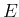 . Note
that the role of
. Note
that the role of 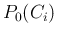 was explicitly considered by Laplace, who 1) before
gave the rule in the case of
was explicitly considered by Laplace, who 1) before
gave the rule in the case of 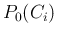 numerically all equal, which then drop
from Eq. (
numerically all equal, which then drop
from Eq. (![[*]](crossref.png) ); 2) then specified that “if these various
causes, considered à priori, are unequally probable,
it is necessary, in the place of the probability of the event resulting from
each cause, to employ the product
of this probability by the possibility of the cause itself.”
(Here `possibility' and `probability' are clearly used as synonyms.)
Then, the importance of the finding is stressed:
); 2) then specified that “if these various
causes, considered à priori, are unequally probable,
it is necessary, in the place of the probability of the event resulting from
each cause, to employ the product
of this probability by the possibility of the cause itself.”
(Here `possibility' and `probability' are clearly used as synonyms.)
Then, the importance of the finding is stressed:
“This is the fundamental principle of this branch of the analysis
of chances which consists in passing from events to causes.”
Generalizing this `principle' to an infinite number of causes,
associated to all possible values of the parameter 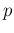 , with the
`event' being the observation of
, with the
`event' being the observation of 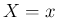 successes in
successes in 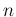 trials,
we get the case sketched in the right
diagram of Fig.
trials,
we get the case sketched in the right
diagram of Fig. ![[*]](crossref.png) , in which the unobserved
node is now
, in which the unobserved
node is now 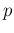 .
Equation (
.
Equation (![[*]](crossref.png) ) becomes then,
in terms of the probability function of
) becomes then,
in terms of the probability function of 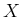 and of the
pdf of
and of the
pdf of 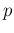
 for which we take the freedom
of using the same symbol `
for which we take the freedom
of using the same symbol `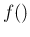 '
'![$]$](img124.png) ,
,
- The Seventh Principle then states that “the probability of
a future event is the sum of the products of the probability of each cause,
drawn from the event observed, by the probability that, this cause existing, the future
event will occur”, that is
Generalizing also this `principle' to an infinite number of causes
associated to all possible values of the parameter 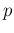 we get Eq. (
we get Eq. (![[*]](crossref.png) ), and then Eq. (
), and then Eq. (![[*]](crossref.png) ):
the probability of interest is the mean of the distribution of
):
the probability of interest is the mean of the distribution of 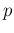 .
.
The solution of Eq. (![[*]](crossref.png) ), in the case
), in the case
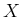 is described by Eq. (
is described by Eq. (![[*]](crossref.png) ) and
we consider
all values of
) and
we consider
all values of 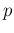 à priori equally likely, is a Beta pdf,
that is12
à priori equally likely, is a Beta pdf,
that is12
with 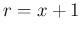 and
and 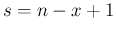 .
Mean value
and variance of the possible values of
.
Mean value
and variance of the possible values of 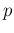 are then
are then
Finally, using Eq. (![[*]](crossref.png) ) and Eq. (
) and Eq. (![[*]](crossref.png) )
we get the Laplace's rule of succession
)
we get the Laplace's rule of succession
Thus, in the special case of `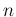 successes in
successes in 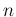 trials',
“we find that an event having occurred successively any
number of times, the probability that it will happen
again the next time is equal to this number increased
by unity divided by the same number, increased by two units” [23],
i.e.
trials',
“we find that an event having occurred successively any
number of times, the probability that it will happen
again the next time is equal to this number increased
by unity divided by the same number, increased by two units” [23],
i.e.
In the case of 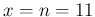 we have then
12/13, or 92.3%. Reporting thus
100% (see footnote
we have then
12/13, or 92.3%. Reporting thus
100% (see footnote ![[*]](crossref.png) )
can be at least misleading,
especially because such a value can be (as it has indeed been)
nowadays promptly broadcasted uncritically
by the media (see e.g. [16] - we have heard
so far no criticism in the media of such an incredible claim,
but only sarcastic comments by colleagues).
)
can be at least misleading,
especially because such a value can be (as it has indeed been)
nowadays promptly broadcasted uncritically
by the media (see e.g. [16] - we have heard
so far no criticism in the media of such an incredible claim,
but only sarcastic comments by colleagues).
![]() ') events of a given kind
occur in
') events of a given kind
occur in ![]() trials, assuming that
trials, assuming that ![]() remains constant. The result is given by the
well known binomial, that is
remains constant. The result is given by the
well known binomial, that is
![[*]](crossref.png) .
.
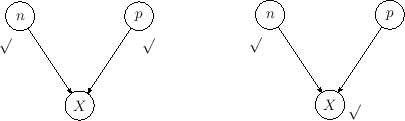
![[*]](crossref.png) ); 2) then specified that “if these various
causes, considered à priori, are unequally probable,
it is necessary, in the place of the probability of the event resulting from
each cause, to employ the product
of this probability by the possibility of the cause itself.”
(Here `possibility' and `probability' are clearly used as synonyms.)
Then, the importance of the finding is stressed:
); 2) then specified that “if these various
causes, considered à priori, are unequally probable,
it is necessary, in the place of the probability of the event resulting from
each cause, to employ the product
of this probability by the possibility of the cause itself.”
(Here `possibility' and `probability' are clearly used as synonyms.)
Then, the importance of the finding is stressed:
![[*]](crossref.png) , in which the unobserved
node is now
, in which the unobserved
node is now ![[*]](crossref.png) ) becomes then,
in terms of the probability function of
) becomes then,
in terms of the probability function of ![[*]](crossref.png) ), and then Eq. (
), and then Eq. (![[*]](crossref.png) ):
the probability of interest is the mean of the distribution of
):
the probability of interest is the mean of the distribution of ![[*]](crossref.png) ), in the case
), in the case
![[*]](crossref.png) ) and
we consider
all values of
) and
we consider
all values of ![[*]](crossref.png) ) and Eq. (
) and Eq. (![[*]](crossref.png) )
we get the Laplace's rule of succession
)
we get the Laplace's rule of succession
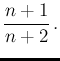
![[*]](crossref.png) )
can be at least misleading,
especially because such a value can be (as it has indeed been)
nowadays promptly broadcasted uncritically
by the media (see e.g. [16] - we have heard
so far no criticism in the media of such an incredible claim,
but only sarcastic comments by colleagues).
)
can be at least misleading,
especially because such a value can be (as it has indeed been)
nowadays promptly broadcasted uncritically
by the media (see e.g. [16] - we have heard
so far no criticism in the media of such an incredible claim,
but only sarcastic comments by colleagues).