Beta approximation of the MCMC results
and its utility
Moving to our results about the `model parameter 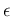 '
(it is now time to be more careful with names), reported
in Tab.
'
(it is now time to be more careful with names), reported
in Tab. ![[*]](crossref.png) and Fig.
and Fig. ![[*]](crossref.png) ,
it should now be clear why the number to report as efficacy
should be the mean of the distribution. As far as the distribution
of
,
it should now be clear why the number to report as efficacy
should be the mean of the distribution. As far as the distribution
of 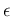 is concerned, given the similarity of the inferential problem
that was first solved by Bayes and Laplace, we have good reasons
to expect that it should not `differ much' from
a Beta. In order to test the correctness of our guess we have done the
simple exercise of superimposing over the MCMC distributions
of Fig.
is concerned, given the similarity of the inferential problem
that was first solved by Bayes and Laplace, we have good reasons
to expect that it should not `differ much' from
a Beta. In order to test the correctness of our guess we have done the
simple exercise of superimposing over the MCMC distributions
of Fig. ![[*]](crossref.png) the Beta pdf's evaluated
from mean and standard deviation of Tab.
the Beta pdf's evaluated
from mean and standard deviation of Tab. ![[*]](crossref.png) .
The distribution parameters can be
in fact obtained solving Eqs. (
.
The distribution parameters can be
in fact obtained solving Eqs. (![[*]](crossref.png) ) - (
) - (![[*]](crossref.png) )
for
)
for 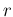 and
and 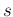 :13
:13
Figure:
MCMC inferred distributions of 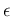 (solid lines exactly as in Fig.
(solid lines exactly as in Fig. ![[*]](crossref.png) ) with superimposed
(dashed lines, often coinciding with the solid ones)
the corresponding Beta distributions evaluated from
the mean values and the standard deviations resulting from MCMC.
) with superimposed
(dashed lines, often coinciding with the solid ones)
the corresponding Beta distributions evaluated from
the mean values and the standard deviations resulting from MCMC.
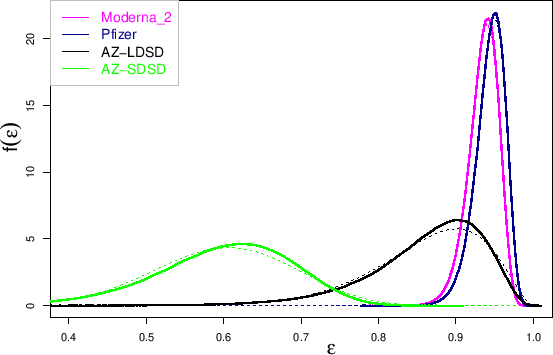 |
The result is shown in Fig. ![[*]](crossref.png) .
As we can see, the agreement is rather good for all cases,
especially for Moderna and Pfizer, for which the Beta and MCMC curves
practically coincide.
.
As we can see, the agreement is rather good for all cases,
especially for Moderna and Pfizer, for which the Beta and MCMC curves
practically coincide.
Subsections
![[*]](crossref.png) and Fig.
and Fig. ![[*]](crossref.png) ,
it should now be clear why the number to report as efficacy
should be the mean of the distribution. As far as the distribution
of
,
it should now be clear why the number to report as efficacy
should be the mean of the distribution. As far as the distribution
of ![[*]](crossref.png) the Beta pdf's evaluated
from mean and standard deviation of Tab.
the Beta pdf's evaluated
from mean and standard deviation of Tab. ![[*]](crossref.png) .
The distribution parameters can be
in fact obtained solving Eqs. (
.
The distribution parameters can be
in fact obtained solving Eqs. (![[*]](crossref.png) ) - (
) - (![[*]](crossref.png) )
for
)
for ![[*]](crossref.png) .
As we can see, the agreement is rather good for all cases,
especially for Moderna and Pfizer, for which the Beta and MCMC curves
practically coincide.
.
As we can see, the agreement is rather good for all cases,
especially for Moderna and Pfizer, for which the Beta and MCMC curves
practically coincide.