@skip

title

author

Abstract:

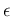
Based on the information communicated in press releases, and finally published towards the end of 2020 by Pfizer, Moderna and AstraZeneca, we have built up a simple Bayesian model, in which the main quantity of interest plays the role of vaccine efficacy (`$\epsilon$'). The resulting Bayesian Network is processed by a Markov Chain Monte Carlo (MCMC), implemented in JAGS interfaced to R via rjags. 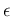As outcome, we get several probability density functions (pdf's) of $\epsilon$, each conditioned on the data provided by the three pharma companies. The result is rather stable against large variations of the number of people participating in the trials and it is `somehow' in good agreement with the results provided by the companies, in the sense that their values correspond to the most probable value (`mode') of the pdf's resulting from MCMC, thus reassuring us about the validity of our simple model. However we maintain that the number to be reported as vaccine efficacy should be the mean of the distribution, rather than the mode, as it was already very clear to Laplace about 250 years ago (its `rule of succession' follows from the simplest problem of the kind). This is particularly important in the case in which the number of successes equals the numbers of trials, as it happens with the efficacy against `severe forms' of infection, claimed by Moderna to be 100%. The implication of the various uncertainties on the predicted number of vaccinated infectees is also shown, using both MCMC and approximated formulae.

“...the most important questions of life ...

are indeed for the most part only problems in probability”

“we find that an event having occurred successively

any number of times, the probability that it will happen again

the next time is equal to this number increased by unity

divided by the same number, increased by two units”

(Laplace)