Since this paper can be seen as the sequel of Refs. [12]
and [9], with the basic considerations already
expounded in [8], for the convenience of the reader I
shortly summarize the main points maintained there.
- The ``essential problem of the experimental method''
is nothing but solving ``a problem in the probability of causes'',
i.e. ranking in credibility the hypotheses
that are considered to be possibly responsible of the observations,
(quotes by Poincaré[13]).3
 There is indeed
no conceptual difference between ``comparing hypotheses''
or ``inferring the value'' of a physical quantity, the two problems
only differing in the numerosity of hypotheses, virtually
infinite in the latter case, when the physical quantity is
assumed, for mathematical
convenience,4
to assume values with
continuity.
There is indeed
no conceptual difference between ``comparing hypotheses''
or ``inferring the value'' of a physical quantity, the two problems
only differing in the numerosity of hypotheses, virtually
infinite in the latter case, when the physical quantity is
assumed, for mathematical
convenience,4
to assume values with
continuity.![$]$](img29.png)
- The deep source of uncertainty in inference is due
to the fact that (apparently) identical causes
might produce different effects, due to
internal (intrinsic) probabilistic aspects of the theory,
as well as to external factors (think at measurement errors).
- Humankind is used to live - and survive -
in conditions of uncertainty and therefore the human mind
has developed a mental
`category' to handle it: probability,
meant as degree of belief. This is also valid when we `make science',
since ``it is scientific only to say what is more likely
and what is less likely'' (Feynman[15]).
- Falsificationism
can be recognized as an attempt to extend
the classical proof by contradiction of classical logic
to the experimental method, but it simply fails when
stochastic (either internal or external) effects might occur.
- The further extension of falsificationism from
impossible effects to improbable effects is
simply deleterious.
- The invention of p-values can be seen as
an attempt to overcome the evident problem occurring in the case
of a large number of effects (virtually infinite when
we make measurements): any observation has a very small probability
in the light of whatever hypothesis is considered, and then
it `falsifies' it.
- Logically the previous extension (``observed effect''
 ``all possible effects equally or less probable than the observed one'')
does not hold water.
(But it seems that for many practitioners logic is optional -
the reason why ``p-values often work''[8]
will be discussed in
section 6.)
``all possible effects equally or less probable than the observed one'')
does not hold water.
(But it seems that for many practitioners logic is optional -
the reason why ``p-values often work''[8]
will be discussed in
section 6.)
- In practice p-values are routinely misinterpreted by most
practitioners and scientists, and
incorrect interpretations of the data are spread around over the
media5 (for recent
examples, related to the LHC presumptive
750GeV di-photon signal (see
e.g. [16,17,18,19,20] and footnote 31 for later comments.).
- The reason of the misunderstandings is that
p-values (as well as other outcomes from other methods of
the dominating `standard statistics', including
confidence intervals[8]),
do not reply to the very question human minds
by nature ask for, i.e. which hypothesis is more or less
believable (or how likely the `true' value
of a quantity lies within a given interval).
For this reason
I am afraid p-values (or perhaps a new invention by statisticians)
will still be misinterpreted
and misused despite the 2016 ASA statement, as I will argue at the
end of section 3.2).
- Given the importance of the previous point,
for the convenience of the reader I report here
verbatim the list of misunderstandings appearing in the
Wikipedia at the end of 2011[9],6
highlighting the sentences that mostly concern our
discourse.
- ``The p-value is not the probability that the null hypothesis is true.
In fact, frequentist statistics does not, and cannot,
attach probabilities to hypotheses. Comparison of Bayesian
and classical approaches shows that a p-value can be very close
to zero while the posterior probability of the null is very close
to unity (if there is no alternative hypothesis with a large
enough a priori probability and which would explain the results
more easily). This is the Jeffreys-Lindley paradox.
- The p-value is not the probability that a finding is
``merely a fluke.''
As the calculation of a p-value is based on the assumption that
a finding is the product of chance alone, it patently cannot also
be used to gauge the probability of that assumption being true.
This is different from the real meaning which is that the p-value
is the chance of obtaining such results if the null hypothesis is true.
- The p-value is not the probability of falsely rejecting
the null hypothesis. This error is a version of the so-called
prosecutor's fallacy.
- The p-value is not the probability that a replicating
experiment would not yield the same conclusion.
-
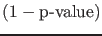 is not the probability of the
alternative hypothesis being true.
is not the probability of the
alternative hypothesis being true.
- The significance level of the test is not determined by the p-value.
The significance level of a test is a value that should
be decided upon by the agent interpreting the data before
the data are viewed, and is compared against the p-value
or any other statistic calculated after the test has been performed.
(However, reporting a p-value is more useful than simply saying
that the results were or were not significant at a given level,
and allows the reader to decide for himself whether to consider
the results significant.)
- The p-value does not indicate the size or importance
of the observed effect (compare with effect size).
The two do vary together however - the larger the effect,
the smaller sample size will be required to get a significant p-value.''
- If we want to form our minds about which hypothesis is more or
less probable in the light of all available information, then
we need to base our reasoning on probability theory,
understood as the mathematics of beliefs, that is essentially
going back to the ideas of Laplace. In particular
the updating rule, presently known as the Bayes rule
(or Bayes theorem), should be probably better called
Laplace rule, or at least Bayes-Laplace rule.
- The `rule', expressed
in terms of the alternative causes
(
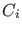 ) which could possibly produce the effect (
) which could possibly produce the effect (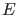 ),
as originally done by Laplace,7 is
),
as originally done by Laplace,7 is
or, considering also
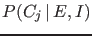 and taking the ratio of
the two
posterior probabilities,
and taking the ratio of
the two
posterior probabilities,
where 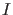 stands for the background information,
sometimes implicitly assumed.
stands for the background information,
sometimes implicitly assumed.
- Important consequences of this rule - I like to call them
Laplace's teachings[9], because they stem
from his ``fundamental principle of that branch of
the analysis of chance that consists of reasoning a
posteriori from events to causes''[23] -
are:
- It makes no sense to speak about how the probability
of
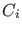 changes if:
changes if:
- there is no alternative cause
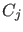 ;
;
- the way how
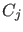 might produce
might produce 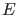 is not
properly modelled,
i.e. if
is not
properly modelled,
i.e. if
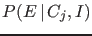 has not been somehow
assessed.8
has not been somehow
assessed.8
- The updating of the probability ratio
depends only on the so called Bayes factor
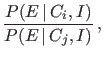 |
|
|
(3) |
ratio of the probabilities of 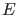 given either
hypotheses,9
and not on the probability of other
events that have not been observed and
that are even less probable than
given either
hypotheses,9
and not on the probability of other
events that have not been observed and
that are even less probable than 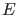 (upon which
p-values are instead calculated).
(upon which
p-values are instead calculated).
- One should be careful not to confuse
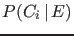 with
with 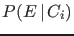 , and in general
, and in general 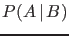 ,
with
,
with 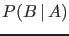 . Or, moving to continuous variables,
. Or, moving to continuous variables,
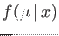 with
with 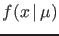 , where: `
, where: `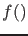 ' stands here,
depending on the contest,
for a probability function
or for a probability density function (pdf):
' stands here,
depending on the contest,
for a probability function
or for a probability density function (pdf):
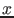 and
and 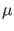 are symbols for observed quantity and
`true' value, respectively, the latter being in fact just
the parameter of the model we use to describe the physical
world.
are symbols for observed quantity and
`true' value, respectively, the latter being in fact just
the parameter of the model we use to describe the physical
world.
- Cause
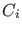 is falsified by the observation
of the event
is falsified by the observation
of the event 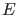 only if
only if
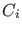 cannot produce it, and not
because of the smallness of
cannot produce it, and not
because of the smallness of
 .
.
- Extending the reasoning to continuous observables (generically
called
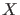 )
characterized by a pdf
)
characterized by a pdf
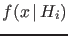 , the probability to observe a value in the
small interval
, the probability to observe a value in the
small interval 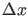 is
is
 .
What matters, for the comparison of two hypotheses in the light
of the observation
.
What matters, for the comparison of two hypotheses in the light
of the observation 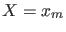 , is
therefore
the ratio of pdf's
, is
therefore
the ratio of pdf's
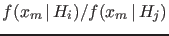 , and not
the smallness of
, and not
the smallness of
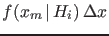 , which tends
to zero as
, which tends
to zero as
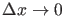 . Therefore,
an hypothesis is, strictly speaking, falsified,
in the light
of the observed
. Therefore,
an hypothesis is, strictly speaking, falsified,
in the light
of the observed 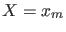 , only if
, only if
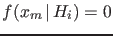 .
.
- Finally, I would like to stress that falsificability
is not a strict
requirement for a theory to be accepted as
`scientific'.
In fact, in my opinion a weaker condition is sufficient,
which I called testability in [12]:
given a theory
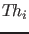 and possible observational data
and possible observational data
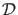 , it should be possible to model
, it should be possible to model
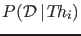 in order to compare it
with an alternative theory
in order to compare it
with an alternative theory 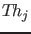 characterized
by
characterized
by
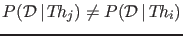 .10
This will allow to rank theories in probability in the light
of empirical data and of any other criteria, like
simplicity or aesthetics11
without the requirement of falsification, that cannot be achieved,
logically speaking,
in most cases.12
.10
This will allow to rank theories in probability in the light
of empirical data and of any other criteria, like
simplicity or aesthetics11
without the requirement of falsification, that cannot be achieved,
logically speaking,
in most cases.12
Giulio D'Agostini
2016-09-06