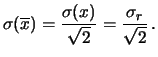C'è infine un terzo modo di procedere,
euristico, in quanto assume che la soluzione
di prova sia quella buona e fornisce soltanto il valore dell'incertezza.
Per semplicità illustriamo questo (per gli altri c'è poco
da spiegare, si tratta solo di fare i conti...).
Assumiamo, ragionevolmente,
che il valore centrale intorno al quale è distribuito
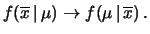 sia la media aritmetica:
sia la media aritmetica:
Subordinatamente ad un certo valore di 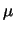 anche la media
aritmetica
anche la media
aritmetica
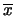 è una variabile casuale, in quanto
è funzione di variabili casuali. Anch'essa, per simmetria,
ha una distribuzione di probabilità intorno a
è una variabile casuale, in quanto
è funzione di variabili casuali. Anch'essa, per simmetria,
ha una distribuzione di probabilità intorno a 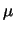 .
In questo caso il processo di inferenza è
del tipo10.3
La differenza rispetto al caso precedente è nella diversa
deviazione standard di
.
In questo caso il processo di inferenza è
del tipo10.3
La differenza rispetto al caso precedente è nella diversa
deviazione standard di
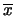 intorno
a
intorno
a 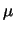 .
Anche se per arrivare all'esatto fattore
di riduzione si rimanda ad un testo di calcolo delle
probabilità (vedi anche Appendice),
il risultato può essere giusticato dicendo che, essendo
.
Anche se per arrivare all'esatto fattore
di riduzione si rimanda ad un testo di calcolo delle
probabilità (vedi anche Appendice),
il risultato può essere giusticato dicendo che, essendo
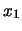 e
e 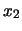 indipendenti, le fluttuazioni della media
tendono a compensarsi.
Quantitativamente si ottiene che
Quindi, utilizzando ancora una volta il ragionamento
di inversione di probabilità intuitivo, possiamo
dire che
indipendenti, le fluttuazioni della media
tendono a compensarsi.
Quantitativamente si ottiene che
Quindi, utilizzando ancora una volta il ragionamento
di inversione di probabilità intuitivo, possiamo
dire che
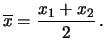
![]() sia la media aritmetica:
sia la media aritmetica: