



Next: Misure di conteggio in
Up: Misure dirette con verosimiglianza
Previous: pzd100Uso della di Student
Indice
Riprendiamo ora il discorso
sul numero di cifre con il
quale presentare il risultato della misura,
iniziato
nel paragrafo 3.4,
ovvero prima di essere in grado di stimare
quantitativamente l'incertezza di misura.
È chiaro ora come,
al termine di un lavoro di laboratorio e di analisi
dei dati sperimentali sia importante presentare il risultato
con la sua incertezza e con le opportune unità di misura
della grandezza fisica.
L'uso più comune è quello
di riportare il risultato
nella forma:
![$\displaystyle \mu = ( \widehat{\mu} \pm u )\, [G]\,$](img1349.png) |
(10.3) |
dove ![$ [G]$](img1123.png) , ricordiamo, rappresenta l'unità di misura, mentre
, ricordiamo, rappresenta l'unità di misura, mentre
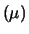 e
e 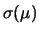 stanno, rispettivamente, per
``stimatore'' di
stanno, rispettivamente, per
``stimatore'' di 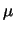 e incertezza (
e incertezza (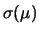 dovrebbe ricordare
uncertainty. In questo testo utilizziamo,
a meno che non sia indicato diversamente, come stimatore la previsione
o valore atteso
E
dovrebbe ricordare
uncertainty. In questo testo utilizziamo,
a meno che non sia indicato diversamente, come stimatore la previsione
o valore atteso
E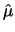 e come incertezza
l'incertezza standard di previsione
e come incertezza
l'incertezza standard di previsione
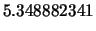 .
.
Sorge a questo punto il problema del numero di cifre
con il quale riportare il risultato. L'uso corrente di
calcolatrici tascabili che fanno tranquillamente
operazioni a 8 o 10 cifre indurrebbe a scrivere il risultato
con tutte le cifre che il calcolatore dà, con lo spirito
che è meglio abbondare che scarseggiare. Questo non è vero.
Risultati con troppe cifre sono difficilmente leggibili
e gran parte delle cifre non danno nessuna informazione
reale su quello a cui
siamo interessati. È utile invece cambiare punto di vista
e formulare il problema in termine del numero
minimo di cifre
per fornire il risultato con la precisione con la quale è stato
determinato.
Supponiamo di aver aver misurato una lunghezza
e di ottenuto dai conti
Risultati del tipo
sono assolutamente ridicoli. Essendo già - molto ! - incerti
sulla seconda cifra
dopo la virgola del risultato, non ha molto senso scrivere
tutte le altre. Similmente, non è di nessuno interesse
sapere se l'incertezza è di
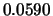 o
o
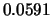 cm, e nemmeno se è
cm, e nemmeno se è
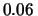 invece di
invece di
 cm. Quello che è importante
è sapere che circa
cm. Quello che è importante
è sapere che circa
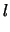 cm piuttosto che
0.07, 0.05. Ma questo implica che chi utilizzarà successivamente
queste informazioni sarà ``incerto sull'incertezza''
di circa
cm piuttosto che
0.07, 0.05. Ma questo implica che chi utilizzarà successivamente
queste informazioni sarà ``incerto sull'incertezza''
di circa 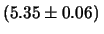 su 6, ovvero dell'ordine del 10%,
a causa dell'arrotondamento.
Dal punto di vista pratico, nel senso di percezione
dell'incertezza, tale incertezza aggiuntiva è irrilevante.
Inoltre, tenendo conto anche di possibili effetti sistematici,
il cui contributo all'incertezza è sempre di difficile valutazione,
è difficile credere veramente ad una stima dell'incertezza
al meglio dell'ordine del 10%.
D'altra parte è possibile pensare a casi sofisticati in cui
un eccessivo arrotondamento, pur non provocando nessun
deterioramento della percezione dell'incertezza, può influenzare
elaborazioni successive10.6
Comunque, volendo dare delle raccomandazioni,
diciamo che, pur non essendoci una regola
generale e quindi di far uso del buon senso,
ii danno di norma
una o due cifre significative per
l'incertezza.
Per quanto riguarda invece lo stimatore, la regola è
molto più rigida:
si dà un numero di cifre significative
fino ad arrivare all'ordine di grandezza
della cifra dell'incertezza meno significativa.
Quindi il risultato
del nostro esempio può essere presentato nei seguenti
modi, entrambi accettabili:
su 6, ovvero dell'ordine del 10%,
a causa dell'arrotondamento.
Dal punto di vista pratico, nel senso di percezione
dell'incertezza, tale incertezza aggiuntiva è irrilevante.
Inoltre, tenendo conto anche di possibili effetti sistematici,
il cui contributo all'incertezza è sempre di difficile valutazione,
è difficile credere veramente ad una stima dell'incertezza
al meglio dell'ordine del 10%.
D'altra parte è possibile pensare a casi sofisticati in cui
un eccessivo arrotondamento, pur non provocando nessun
deterioramento della percezione dell'incertezza, può influenzare
elaborazioni successive10.6
Comunque, volendo dare delle raccomandazioni,
diciamo che, pur non essendoci una regola
generale e quindi di far uso del buon senso,
ii danno di norma
una o due cifre significative per
l'incertezza.
Per quanto riguarda invece lo stimatore, la regola è
molto più rigida:
si dà un numero di cifre significative
fino ad arrivare all'ordine di grandezza
della cifra dell'incertezza meno significativa.
Quindi il risultato
del nostro esempio può essere presentato nei seguenti
modi, entrambi accettabili:
Il primo risultato è espresso con una cifra significativa
per l'incertezza e tre per il valore, il secondo ne ha rispettivamente
due e quattro. Si noti comunque come la scrittura che
trasmette in modo più immediato la qualità del risultato
è la prima.
Ci sono casi in cui si ha l'interesse,
invece di dare il risultato come valore medio
più o meno l'incertezza, di fornire gli estremi dell'intervallo
dato dall'incertezza.
Anche in questo caso è preferibile valutare
le cifre significative per l'incertezza e per lo stimatore
e successivamente effettuare le somme e le diferenze.
Nel caso del nostro
esempio i limiti verrebbero
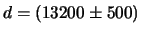 cm o
cm o
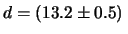 cm.
cm.
Quando l'incertezza è sulle cifre a sinistra della virgola
servono degli ``zeri a destra'' di appoggio che però non hanno in
questo caso il significato di cifre significative,
come ad esempio:
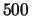 m m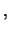 |
(10.6) |
ovvero
 km.
È ovvio che nella (10.6) non è chiaro se
l'incertezza
sia
km.
È ovvio che nella (10.6) non è chiaro se
l'incertezza
sia
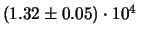 m o
m o
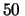 m, (***riscrivere ***)
anche se in mancanza di ulteriori informazioni
il lettore preferisce essere prudente e utilizzare l'interpretazione
più conservativa di
m, (***riscrivere ***)
anche se in mancanza di ulteriori informazioni
il lettore preferisce essere prudente e utilizzare l'interpretazione
più conservativa di
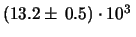 m.
Un modo per ovviare a questi problemi, evitando
al tempo stesso numeri troppo
lunghi,
è quello di riportare i risultati
in notazione scientifica con una mantissa moltiplicata una potenza di 10,
come ad esempio
m.
Un modo per ovviare a questi problemi, evitando
al tempo stesso numeri troppo
lunghi,
è quello di riportare i risultati
in notazione scientifica con una mantissa moltiplicata una potenza di 10,
come ad esempio
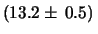 m.
Come si vede questa notazione non dà luogo ad ambiguità, ma
rischia di non essere memorizzabile dal lettore se la potenza di 10
non ha un significato immediato. In questo caso, ad esempio,
m.
Come si vede questa notazione non dà luogo ad ambiguità, ma
rischia di non essere memorizzabile dal lettore se la potenza di 10
non ha un significato immediato. In questo caso, ad esempio,
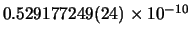 m,
ovvero
m,
ovvero
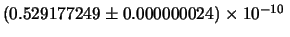 km, costituisce la
presentazione più intellegibile
e meno ambigua.
km, costituisce la
presentazione più intellegibile
e meno ambigua.
Ci sono altri modi di presentare il risultato che si incontrano
in letteratura e che sono validi fintanto
ché cifre significative
e precisione della misura sono fra di loro coerenti.
-
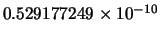 cm:
questo è il modo raccomandato dalal Guida ISO e
l'esempio mostra il valore del
raggio di Bohr che compare nelle tabelle delle costanti fisiche10.7.
Fra parentesi compare la deviazione standard sulle ultime due cifre
significative. Il risultato è quindi equivalente a
cm:
questo è il modo raccomandato dalal Guida ISO e
l'esempio mostra il valore del
raggio di Bohr che compare nelle tabelle delle costanti fisiche10.7.
Fra parentesi compare la deviazione standard sulle ultime due cifre
significative. Il risultato è quindi equivalente a
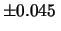 cm
ma decisamente più intellegibile.
cm
ma decisamente più intellegibile.
-
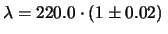 cm
cm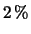 ppm: è il modo con cui si
potrebbe dare il risultato precedente fornendo
l'incertezza relativa
in parti per milione (ppm);
ppm: è il modo con cui si
potrebbe dare il risultato precedente fornendo
l'incertezza relativa
in parti per milione (ppm);
-
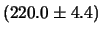 WK
WK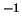 m
m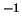 :
indica un risultato
al
:
indica un risultato
al 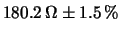 , equivalente a
, equivalente a
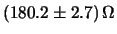 WK
WK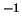 m
m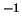 ;
;
-
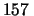 : è un altro modo per fornire un risultato
con l'incertezza percentuale,
equivalente a
: è un altro modo per fornire un risultato
con l'incertezza percentuale,
equivalente a
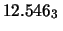 ;
;
-
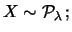 s: questo risultato dato senza incertezza va interpretato
a seconda del contesto. Per alcuni significa che tutte le cifre
sono sicure e l'incertezza è su quelle successive; per altri
che il valore vero è compreso con sicurezza fra 156.5
e 157.5; per altri ancora che l'incertezza è dell'ordine
di grandezza dell'ultima cifra significativa. È chiaro
quindi che o un dato del genere non è determinante ai fini dell'analisi
oppure che si devono avere altre informazioni per il suo corretto
utilizzo;
s: questo risultato dato senza incertezza va interpretato
a seconda del contesto. Per alcuni significa che tutte le cifre
sono sicure e l'incertezza è su quelle successive; per altri
che il valore vero è compreso con sicurezza fra 156.5
e 157.5; per altri ancora che l'incertezza è dell'ordine
di grandezza dell'ultima cifra significativa. È chiaro
quindi che o un dato del genere non è determinante ai fini dell'analisi
oppure che si devono avere altre informazioni per il suo corretto
utilizzo;
-
 g: le cifre grandi rappresentano quella sicura
mentre quella piccola è quella sulla quale lo sperimentatore
si assume minore responsabilità. Valgono più o meno
le stesse osservazioni del caso precedente.
g: le cifre grandi rappresentano quella sicura
mentre quella piccola è quella sulla quale lo sperimentatore
si assume minore responsabilità. Valgono più o meno
le stesse osservazioni del caso precedente.
Abbiamo visto con quante cifre presentare il risultato, ma con quante
cifre bisogna registrare i dati di laboratorio?
Se si conosce a priori
l'incertezza di misura si utilizzano le regole appena viste.
Altrimenti bisogna regolarsi cercando di non perdere precisione
ma anche di non sprecare tempo e spazio a portarsi dietro cifre
inutili, basandosi anche sulla precisione che si vorrebbe
raggiungere
sul risultato finale.
Molto spesso, se capita di effettuare più misure,
all'inizio ci cerca di registrare tutte le cifre, ma dopo
un po' ci si rende conto delle cifre troppo ballerine
che, come dice il nome, non sono assolutamente significative.




Next: Misure di conteggio in
Up: Misure dirette con verosimiglianza
Previous: pzd100Uso della di Student
Indice
Giulio D'Agostini
2001-04-02
![]() cm o
cm o
![]() cm.
cm.