



Next: pzd100Come tener conto anche
Up: Fit
Previous: Fit
Indice
Supponiamo di aver misurato delle coppie di grandezze fisiche,
di averne osservato l'andamento su un grafico, di avere ipotizzato
il tipo di funzione matematica che lega ascisse e ordinate
e di voler determinare i parametri della funzione. Consideriamo
il semplice caso di un andamento lineare:
ove con 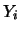 e
e 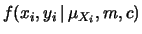 sono i valori veri delle grandezze.
sono i valori veri delle grandezze.
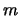 e
e 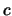 sono parametri di valore ignoto, ovvero numeri aleatori reali
(avremmo dovuto usare le lettere maiuscole, ma, come già fatto
precedentemente in altri casi preferiamo usare lo stesso simbolo con
il quale tali grandezze vengono usualmente indicate).
Indichiamo con
sono parametri di valore ignoto, ovvero numeri aleatori reali
(avremmo dovuto usare le lettere maiuscole, ma, come già fatto
precedentemente in altri casi preferiamo usare lo stesso simbolo con
il quale tali grandezze vengono usualmente indicate).
Indichiamo con 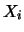 e
e 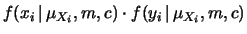 la coppia di valori osservabili,
dati i parametri
la coppia di valori osservabili,
dati i parametri 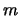 ,
, 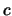 e il valore vero
e il valore vero 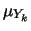 (il
valore vero
(il
valore vero 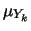 è univocamente determinato dalla
(12.1)), la cui verosimiglianza corrispondente
è data, assumendo un modello normale per gli errori, da
è univocamente determinato dalla
(12.1)), la cui verosimiglianza corrispondente
è data, assumendo un modello normale per gli errori, da
La verosimiglianza acquista una forma più semplice
quando
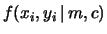 . Infatti ciò significa che
. Infatti ciò significa che
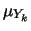 è, dal punto di vista pratico,
univocamente determinata dal valore osservato:
è, dal punto di vista pratico,
univocamente determinata dal valore osservato:
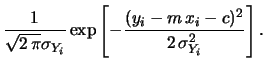 .
La verosimiglianza si
riduce12.1a
.
La verosimiglianza si
riduce12.1a
Se abbiamo tante coppie di valori misurati e le condizioni
sperimentali sono tali che le possibili fluttuazioni delle ordinate intorno
ai loro valori veri sono indipendenti,
abbiamo
ove con
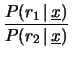 e
e
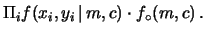 sono stati indicati i vettori
(n-tuple) contenenti i punti osservati.
sono stati indicati i vettori
(n-tuple) contenenti i punti osservati.
Applicando il teorema di Bayes otteniamo finalmente
Assumendo una distribuzione iniziale
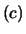 uniforme
e una distribuzione finale circa normale (bivariata),
il problema si riconduce a calcolare il massimo
della distribuzione finale,
che coincide con il massimo della verosimiglianza.
Tale punto di massimo
fornisce
E
uniforme
e una distribuzione finale circa normale (bivariata),
il problema si riconduce a calcolare il massimo
della distribuzione finale,
che coincide con il massimo della verosimiglianza.
Tale punto di massimo
fornisce
E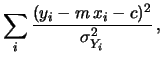 ed
E
ed
E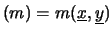 .
In pratica si preferisce massimizzare
il logaritmo della verosimiglianza equivalente a minimizzare
la quantità
come si può verificare facilmente.
Il resto si riduce ad un esercizio di analisi.
.
In pratica si preferisce massimizzare
il logaritmo della verosimiglianza equivalente a minimizzare
la quantità
come si può verificare facilmente.
Il resto si riduce ad un esercizio di analisi.
Avendo ottenuto
E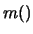 e
E
e
E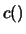 , ove
, ove 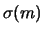 e
e 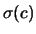 sono le funzioni che legano le migliori stime dei parametri
ai dati sperimentali, si tratta di valutare
sono le funzioni che legano le migliori stime dei parametri
ai dati sperimentali, si tratta di valutare
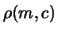 ,
, 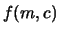 e
e 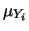 . Essi possono essere
calcolati dalla loro definizione applicata ad
. Essi possono essere
calcolati dalla loro definizione applicata ad 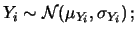 ottenuta dalla (12.5) dopo opportuna normalizzazione.
L'assunzione di approssimazione a normale bivariata di
ottenuta dalla (12.5) dopo opportuna normalizzazione.
L'assunzione di approssimazione a normale bivariata di 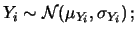 semplifica i calcoli, in quanto i parametri possono essere
ricavati direttamente dalla forma della distribuzione senza
eseguire gli integrali necessari per valutare
semplifica i calcoli, in quanto i parametri possono essere
ricavati direttamente dalla forma della distribuzione senza
eseguire gli integrali necessari per valutare
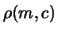
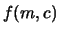 e
e 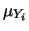 (vedi, ad
esempio, proprietà della distribuzione
normale multivariata nella parte III delle dispense di probabilità).
(vedi, ad
esempio, proprietà della distribuzione
normale multivariata nella parte III delle dispense di probabilità).
Il modo più semplice
per calcolare questi conti è quello di usare un ragionamento
di inversione di probabilità del tipo ``cane-cacciatore'', che
funziona nei limiti che abbiamo più volte indicato
(vedi paragrafo 9.6):




Next: pzd100Come tener conto anche
Up: Fit
Previous: Fit
Indice
Giulio D'Agostini
2001-04-02
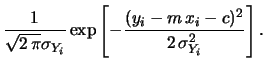 .
La verosimiglianza si
riduce12.1a
.
La verosimiglianza si
riduce12.1a
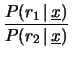 e
e
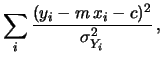 ed
E
ed
E![]() e
E
e
E![]() , ove
, ove ![]() e
e ![]() sono le funzioni che legano le migliori stime dei parametri
ai dati sperimentali, si tratta di valutare
sono le funzioni che legano le migliori stime dei parametri
ai dati sperimentali, si tratta di valutare
![]() ,
, ![]() e
e ![]() . Essi possono essere
calcolati dalla loro definizione applicata ad
. Essi possono essere
calcolati dalla loro definizione applicata ad ![]() ottenuta dalla (12.5) dopo opportuna normalizzazione.
L'assunzione di approssimazione a normale bivariata di
ottenuta dalla (12.5) dopo opportuna normalizzazione.
L'assunzione di approssimazione a normale bivariata di ![]() semplifica i calcoli, in quanto i parametri possono essere
ricavati direttamente dalla forma della distribuzione senza
eseguire gli integrali necessari per valutare
semplifica i calcoli, in quanto i parametri possono essere
ricavati direttamente dalla forma della distribuzione senza
eseguire gli integrali necessari per valutare
![]()
![]() e
e ![]() (vedi, ad
esempio, proprietà della distribuzione
normale multivariata nella parte III delle dispense di probabilità).
(vedi, ad
esempio, proprietà della distribuzione
normale multivariata nella parte III delle dispense di probabilità).