| E |
E |
(12.15) |
| E |
E |
(12.15) |
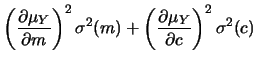 è ottenuta dalla propagazione delle
incertezze, tendendo conto (di fondamentale importanza!)
del termine di correlazione:
è ottenuta dalla propagazione delle
incertezze, tendendo conto (di fondamentale importanza!)
del termine di correlazione:
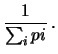 va sostituito nel modo indicato nel
paragrafo precedente se le incertezze sono diverse. Le derivate
vanno calcolate, come solito in corrispondenza di
va sostituito nel modo indicato nel
paragrafo precedente se le incertezze sono diverse. Le derivate
vanno calcolate, come solito in corrispondenza di
Si noti l'andamento di
![]() in funzione di
in funzione di ![]() .
Essa è minima in corrispondenza dei punti sperimentali, in quanto
tutte le informazioni contribuiscono a costringere (probabilisticamente)
il valore di
.
Essa è minima in corrispondenza dei punti sperimentali, in quanto
tutte le informazioni contribuiscono a costringere (probabilisticamente)
il valore di ![]() in un piccolo intervallo intorno alla retta.
A mano a a mano che ci allontana dai punti misurati la qualità
dell'informazione su
in un piccolo intervallo intorno alla retta.
A mano a a mano che ci allontana dai punti misurati la qualità
dell'informazione su ![]() si deteriora,
come indicato molto chiaramente dalla formula 12.16.
. Questo è mostrato in
modo eloquente nella figura 12.1, ove le due
curve tratteggiate indicano la banda di
si deteriora,
come indicato molto chiaramente dalla formula 12.16.
. Questo è mostrato in
modo eloquente nella figura 12.1, ove le due
curve tratteggiate indicano la banda di
 intorno alla retta e quelle puntinate la banda di
di
intorno alla retta e quelle puntinate la banda di
di
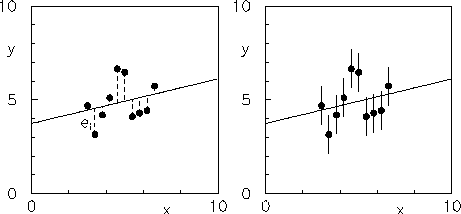 (chiaramente le scale di
(chiaramente le scale di ![]() e di
e di ![]() coincidono).
coincidono).
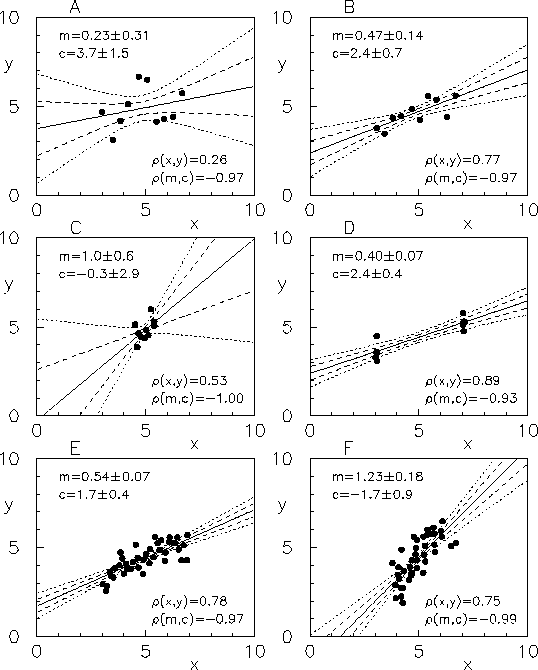
Infine, la figura 12.2 mostra infine la qualità
della determinazione dei parametri e della determinazione di ![]() da
da ![]() a seconda di deviazione standard, numero e
tipo di configurazione dei punti sperimentali.
a seconda di deviazione standard, numero e
tipo di configurazione dei punti sperimentali.