



Next: Proprietà di media e
Up: Descrizione quantitativa dei dati
Previous: Varianza e deviazione standard
Indice
Analogia meccanica di media e
varianza
Si noti come la formula della media pesata (5.7)
ricordi la formula del centro di massa di un corpo esteso,
se si pensa che ogni classe
posta in 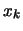 abbia una massa
abbia una massa 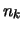 , ovvero un peso (relativo)
, ovvero un peso (relativo) 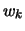 .
Anche la formula (5.6)
per dati non raggruppati ha lo stesso
significato per il caso di
.
Anche la formula (5.6)
per dati non raggruppati ha lo stesso
significato per il caso di 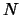 punti di massa unitaria.
Per questa ragione la media aritmetica è spesso chiamata
baricentro della distribuzione. Questa osservazione è anche
importante per stimare ad occhio la media di dati istogrammati:
essa è localizzata nel punto dell'asse delle ascisse
rispetto al quale l'istogramma, visto come un
corpo rigido bidimensionale, si manterrebbe in equilibrio se
sottoposto ad una forza gravitazionale.
punti di massa unitaria.
Per questa ragione la media aritmetica è spesso chiamata
baricentro della distribuzione. Questa osservazione è anche
importante per stimare ad occhio la media di dati istogrammati:
essa è localizzata nel punto dell'asse delle ascisse
rispetto al quale l'istogramma, visto come un
corpo rigido bidimensionale, si manterrebbe in equilibrio se
sottoposto ad una forza gravitazionale.
Anche la varianza ha una semplice interpretazione meccanica,
non essendo altro che il momento di inerzia del corpo rispetto
al baricentro, come si vede dalla
(5.15).
Da queste analogie meccaniche è possibile ottenere interessanti
proprietà della media e della deviazione standard.
- La media è il valore rispetto al quale
è minima la somma dei quadrati degli
scarti.
- Se tutti i punti sono traslati in egual modo anche
la media è traslata della stessa quantità.
- La varianza - e quindi la deviazione standard - è invariante per
traslazione.
- Se tutti i punti vengono moltiplicati per lo stesso
fattore di scala, media
e deviazione standard variano dello stesso fattore.
- Il momento di inerzia rispetto al punto
 è pari al momento
di inerzia rispetto al baricentro più il quadrato della posizione del
baricentro moltiplicata per la massa totale (unitaria) dei punti
sperimentali. Ne segue la seguente propietà:
è pari al momento
di inerzia rispetto al baricentro più il quadrato della posizione del
baricentro moltiplicata per la massa totale (unitaria) dei punti
sperimentali. Ne segue la seguente propietà:
Se si considerano dati sciolti, ciascuno di massa unitaria, si ottiene
Dalle (5.17) e (5.18) (dividendo
quest'ultima per 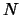 ) si ottiene che
) si ottiene che
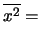 Var Var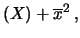 |
(5.19) |
dove con
 si è indicata la media dei quadrati.
Ne segue che
si è indicata la media dei quadrati.
Ne segue che
Var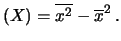 |
(5.20) |
Queste proprietà possono molto utili per semplificare i calcoli
e saranno viste formalmente nel prossimo paragrafo.




Next: Proprietà di media e
Up: Descrizione quantitativa dei dati
Previous: Varianza e deviazione standard
Indice
Giulio D'Agostini
2001-04-02