



Next: Pallinometro
Up: Contatore
Previous: Conteggi a intervalli di
Indice
Nei paragrafi precedenti ci siamo interessati al numero di
conteggi registrati con un contatore a scintillazione avendo
fissato il tempo di lettura. È stata invece persa l'informazione
sulla sequenza temporale degli eventi.
Prima di passare alla misura, cerchiamo di farci un'idea
di cosa ci aspettiamo in base ai dati
della tabella 1.1.
- Il valore di radioattività è `intorno' a 0.18 conteggi al secondo,
ovvero abbiamo in media un conteggio ogni 5.6 secondi.
- Non ci dobbiamo attendere che i conteggi arrivino cadenzati al ritmo
di uno ogni 5.6 secondi, sia perché è difficile immaginare
un meccanismo che controlli
la regolarità dell'arrivo di particelle radioattive provenienti da più
sorgenti, sia perché i dati sperimentali mostrano
grandi fluttuazioni dei tempi di arrivo intorno al
tempo medio di attesa.
- La tabella 1.1 mostra come spesso (11 volte su 100),
anche aspettando 12 secondi (oltre il doppio del tempo medio di attesa),
non si sia verificato nessun evento. A volte
invece (qualche volta ogni cento)
in un tempo
circa la metà di quello medio di attesa si verificano 3 o 4 eventi.
- Si noti inoltre come su tempi lunghi il processo in qualche modo si
regolarizzi: sebbene la variazione fra il minimo e il massimo numero
di conteggi aumenta con il tempo di misura,
il tempo medio
per ogni
singola misura varia molto meno, per esempio va
da 3.8 a 9.1 secondi (78 e 33 eventi in 300 secondi)
nei conteggi registrati in 300 s.
Essendoci convinti che ci aspettiamo un evento ogni 5.6 secondi,
anche se non ci dobbiamo sorprendere se a volte bisogna attendere
molto di più o se altre volte arrivano raffiche di eventi quasi
simultanei, poniamoci ancora delle domande.
- Supponiamo di dividere il tempo di attesa in intervallini di
un secondo e di dover fare una scommessa in cui vince chi indovina
l'intervallino esatto in cui si verificherà il conteggio,
su quale intervallino
converrà puntare? Sul sesto, ovvero quello che è quasi centrato sul
tempo medio di attesa? Detto in altre parole, è più probabile
misurare tempi compresi fra 5 e 6 secondi che misurare tempi compresi fra
0 e 1 secondi, fra 1 e 2, etc.? O, ancora, è più probabile osservare
valori compresi fra 0 e 5.6 secondi o valori maggiori di 5.6 secondi?
- Cosa ci dobbiamo aspettare se ci interessiamo
invece al tempo di attesa per registrare
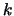 conteggi? È ragionevole pensare che il tempo medio
di attesa sia
conteggi? È ragionevole pensare che il tempo medio
di attesa sia 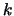 volte quello necessario per il primo conteggio?
Come saranno le fluttuazioni intorno a tale valore?
volte quello necessario per il primo conteggio?
Come saranno le fluttuazioni intorno a tale valore?
Anche per queste domande cerchiamo delle risposte intuitive:
- il tempo di attesa non può essere negativo, ma può essere
arbitrariamente
grande (anche se le grandissime fluttuazioni sembrano molto poco
probabili).
Quindi il numero
di intervallini è infinito. Ma essendo la media nel sesto intervallino,
ci aspettiamo che gli intervallini al si sotto di esso si verifichino
con frequenza superiore di quelli al di sopra in modo tale da compensare,
nel calcolo della media, i grandi tempi di questi ultimi.
Tabella:
Tempi di attesa per osservare un numero prefissato
di eventi. Questi dati simulano quelli ottenibili con contatore
che lavori nelle stesse condizioni di quello con cui sono stati
ottenuti i dati di tabella 1.1.
|
1 conteggio |
|
6.9 |
6.2 |
4.8 |
12.1 |
17.2 |
6.6 |
10.5 |
3.0 |
17.2 |
0.2 |
|
1.5 |
0.6 |
11.5 |
1.7 |
1.7 |
3.8 |
2.9 |
5.5 |
4.1 |
8.1 |
|
2.5 |
6.4 |
0.1 |
0.3 |
4.2 |
2.3 |
0.2 |
8.0 |
5.3 |
2.4 |
|
1.8 |
2.9 |
9.6 |
0.4 |
9.6 |
2.6 |
10.4 |
5.3 |
10.2 |
0.4 |
|
17.3 |
0.7 |
3.1 |
11.0 |
9.0 |
1.0 |
5.1 |
1.8 |
6.6 |
2.8 |
|
8.1 |
11.3 |
0.2 |
0.0 |
8.0 |
1.4 |
4.1 |
2.4 |
6.7 |
3.8 |
|
15.0 |
2.1 |
8.9 |
0.0 |
0.3 |
5.9 |
2.6 |
1.2 |
3.8 |
20.6 |
|
1.0 |
3.4 |
0.9 |
5.0 |
1.8 |
2.6 |
10.0 |
11.4 |
7.8 |
4.4 |
|
12.6 |
1.9 |
0.8 |
8.0 |
3.8 |
18.8 |
0.6 |
6.2 |
0.9 |
5.7 |
|
3.2 |
4.6 |
2.9 |
0.6 |
2.7 |
5.7 |
0.2 |
14.4 |
8.8 |
1.6 |
|
2 conteggi |
|
1.7 |
17.6 |
26.1 |
2.6 |
9.7 |
30.5 |
19.7 |
14.2 |
17.1 |
9.9 |
|
5.1 |
19.2 |
13.5 |
9.8 |
6.6 |
7.8 |
7.1 |
16.3 |
15.9 |
25.2 |
|
9.9 |
4.1 |
12.0 |
14.8 |
1.1 |
28.0 |
33.8 |
5.8 |
34.3 |
17.1 |
|
11.5 |
1.8 |
12.4 |
14.0 |
2.7 |
2.2 |
16.2 |
7.6 |
0.6 |
9.0 |
|
11.8 |
15.2 |
17.1 |
18.5 |
29.5 |
6.1 |
7.1 |
7.2 |
9.3 |
15.6 |
|
5 conteggi |
|
42.5 |
15.3 |
12.0 |
40.6 |
38.9 |
25.8 |
18.1 |
36.8 |
30.1 |
30.9 |
|
28.2 |
21.6 |
35.8 |
7.6 |
18.8 |
20.6 |
36.8 |
28.9 |
17.9 |
16.1 |
|
38.4 |
19.2 |
25.5 |
43.3 |
16.8 |
16.8 |
48.5 |
21.2 |
30.2 |
24.8 |
|
36.7 |
43.1 |
35.1 |
40.6 |
28.4 |
51.0 |
34.4 |
52.1 |
35.3 |
34.8 |
|
39.0 |
40.6 |
24.5 |
20.5 |
27.7 |
33.4 |
52.2 |
13.3 |
39.4 |
11.6 |
|
10 conteggi |
|
61.0 |
36.0 |
55.6 |
47.6 |
28.4 |
66.8 |
64.5 |
31.4 |
29.7 |
49.9 |
|
67.5 |
42.9 |
62.3 |
57.2 |
70.1 |
73.1 |
25.8 |
46.9 |
43.4 |
47.6 |
|
55.6 |
45.1 |
49.9 |
47.1 |
103.9 |
68.5 |
61.1 |
83.7 |
103.3 |
63.8 |
|
24.5 |
54.6 |
67.9 |
32.9 |
68.8 |
60.2 |
36.9 |
70.5 |
54.1 |
50.4 |
|
35.2 |
85.7 |
50.7 |
45.9 |
89.7 |
51.4 |
64.4 |
109.2 |
58.7 |
76.0 |
|
20 conteggi |
|
115.7 |
136.7 |
86.7 |
145.2 |
160.9 |
121.0 |
110.9 |
98.8 |
94.2 |
87.3 |
|
117.9 |
110.2 |
124.1 |
86.6 |
146.2 |
120.2 |
114.4 |
124.8 |
64.7 |
107.1 |
|
129.7 |
108.4 |
115.7 |
120.8 |
141.8 |
157.7 |
168.7 |
96.0 |
101.1 |
118.4 |
|
82.1 |
80.0 |
98.8 |
140.5 |
78.2 |
128.6 |
150.1 |
114.4 |
83.5 |
120.7 |
|
118.5 |
122.4 |
113.3 |
108.7 |
99.6 |
141.8 |
149.8 |
131.0 |
136.7 |
146.8 |
|
50 conteggi |
|
346 |
228 |
327 |
228 |
209 |
297 |
285 |
291 |
245 |
280 |
|
284 |
272 |
325 |
201 |
286 |
301 |
298 |
335 |
233 |
346 |
|
294 |
296 |
267 |
254 |
240 |
251 |
297 |
244 |
344 |
267 |
|
190 |
265 |
267 |
249 |
225 |
238 |
266 |
286 |
285 |
235 |
|
227 |
305 |
246 |
246 |
296 |
253 |
255 |
286 |
208 |
285 |
|
100 conteggi |
|
590 |
669 |
580 |
586 |
498 |
513 |
629 |
537 |
579 |
568 |
|
627 |
542 |
493 |
527 |
459 |
518 |
629 |
518 |
586 |
619 |
|
516 |
617 |
548 |
586 |
594 |
524 |
564 |
551 |
515 |
558 |
|
549 |
627 |
570 |
575 |
490 |
626 |
533 |
491 |
489 |
529 |
|
488 |
663 |
608 |
545 |
550 |
652 |
574 |
560 |
623 |
623 |
|
Anche se da questi argomenti
non si può concludere l'andamento decrescente della probabilità
in funzione del numero di intervallino (come verificheremo), si può
senz'altro affermare che è più probabile misurare tempi
inferiori che tempi superiori
a quello medio di attesa (anticipando il
risultato esatto: 63% contro 37%);
- è abbastanza naturale
che il tempo medio di attesa debba essere proporzionale al
numero di conteggi. Più complicato è fare affermazioni intuitive
sulle fluttuazioni dei tempi intorno alla media e sulle probabilità
dei vari intervallini. Ciò nonostante sembra abbastanza naturale
attendersi che alla regolarizzazione del processo per grandi tempi
di misura se ne debba accompagnare una analoga per un gran numero
di conteggi. Per esempio, dalla tabella 1.1
per 300 s si vede come fluttuazioni oltre
il
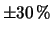 del numero tipico (intorno a 50) siano rare.
Quindi in media bisogna
aspettare circa 300 s per osservare
una cinquantina conteggi, ma dovranno essere
veramente molto rare le fluttuazioni di oltre il doppio o di meno
della metà di tale tempo, cosa invece frequentissima nel caso
di un solo conteggio.
del numero tipico (intorno a 50) siano rare.
Quindi in media bisogna
aspettare circa 300 s per osservare
una cinquantina conteggi, ma dovranno essere
veramente molto rare le fluttuazioni di oltre il doppio o di meno
della metà di tale tempo, cosa invece frequentissima nel caso
di un solo conteggio.
I dati sperimentali (simulati) sono riportati in tabella
1.2. Si notino le enormi fluttuazioni per attendere
il primo conteggio e le minori fluttuazioni relative per registrare
100 conteggi (per un conteggio sono state riportati più valori
``misurati''
per meglio capirne il comportamento).
Per comprendere le ragioni della migliore stabilità per grandi
conteggi è importante la seguente osservazione:
essendo il fenomeno che determina un
conteggio del tutto casuale, si ha la stessa distribuzione di tempi
di attesa sia che si faccia partire il cronometro manualmente
a tempi arbitrari, sia che si prenda per ``start'' del
cronometro l'istante di arrivo dell'ultimo evento. Quindi il tempo
di attesa di  eventi è pari alla somma di
eventi è pari alla somma di  tempi di attesa
di un evento, ognuno indipendente dall'altro. Per questo motivo le enormi
fluttuazioni intorno al tempo di attesa medio tenderanno a
compensarsi,
``in media'', ma non necessariamente!
tempi di attesa
di un evento, ognuno indipendente dall'altro. Per questo motivo le enormi
fluttuazioni intorno al tempo di attesa medio tenderanno a
compensarsi,
``in media'', ma non necessariamente!




Next: Pallinometro
Up: Contatore
Previous: Conteggi a intervalli di
Indice
Giulio D'Agostini
2001-04-02
![]() eventi è pari alla somma di
eventi è pari alla somma di ![]() tempi di attesa
di un evento, ognuno indipendente dall'altro. Per questo motivo le enormi
fluttuazioni intorno al tempo di attesa medio tenderanno a
compensarsi,
``in media'', ma non necessariamente!
tempi di attesa
di un evento, ognuno indipendente dall'altro. Per questo motivo le enormi
fluttuazioni intorno al tempo di attesa medio tenderanno a
compensarsi,
``in media'', ma non necessariamente!