



Next: Distribuzioni di probabilità di
Up: Variabili casuali e distribuzioni
Previous: Ricapitolando
Indice
- Ad un gioco di società si lancia dado. Se il
numero è pari si retrocede di un numero di caselle
pari alla metà del valore indicato; se il numero è dispari
di avanza del doppio del numero indicato. Ricavarsi la distribuzione
di probabilità della variabile casuale ``numero di caselle
delle quali si avanza''.
- Calcolare previone e incertezza di previsione
del numero incerto definito nel
problema precedente.
- Le variabili
 e
e  possono assumere ciascuna cinque valori.
Come distribuzione di probabilità vengono assegnate rispettivamente:
possono assumere ciascuna cinque valori.
Come distribuzione di probabilità vengono assegnate rispettivamente:
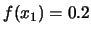 ,
,
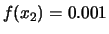 ,
,
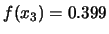 ,
,
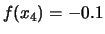 ,
,
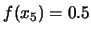 ;
;
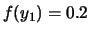 ,
,
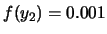 ,
,
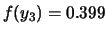 ,
,
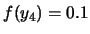 ,
,
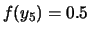 .
.
Cos'è che non va in ciascuna delle distribuzioni?
- Una variabile casuale discreta ha una funzione di ripartizione
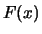 discontinua in corrispondenza dei primi 6 interi positivi.
In tali punti essa assume valori: 0.10, 0.30, 0.60, 0.90, 0.95, 1.00.
Calcolare le seguenti probabilità:
discontinua in corrispondenza dei primi 6 interi positivi.
In tali punti essa assume valori: 0.10, 0.30, 0.60, 0.90, 0.95, 1.00.
Calcolare le seguenti probabilità:
- Si estrae una carta da un mazzo di 40 carte. Quanto vale la
distribuzione di probabilità dei valori delle carte?
Calcolare media e deviazione standard della
distribuzione.
- Si lanciano due dadi. Associare alla variabile
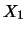 la somma
dei valori che appaiono sulle facce
rivolte verso l'alto e alla
variabile
la somma
dei valori che appaiono sulle facce
rivolte verso l'alto e alla
variabile 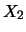 il modulo della loro differenza.
Ricavarsi la distribuzione di probabilità delle
due variabili casuali con i rispettivi valori
di previsione e incertezza di previsione.
il modulo della loro differenza.
Ricavarsi la distribuzione di probabilità delle
due variabili casuali con i rispettivi valori
di previsione e incertezza di previsione.
-
 Uno sperimentatore misura due tensioni di un circuito
con un voltmetro digitale in grado di indicare fino al decimo
di Volt. Lo sperimentatore sa che la misura non è affetta
da errori sistematici, che
lo strumento è ben calibrato e che l'indicazione è effettuata
arrotondando le cifre successive a quella indicata
secondo le regole ``delle calcolatrici tascabili'' (fino
a 4 approssima per difetto, dal 5 - compreso - in poi per eccesso).
Se lo sperimentatore legge
Uno sperimentatore misura due tensioni di un circuito
con un voltmetro digitale in grado di indicare fino al decimo
di Volt. Lo sperimentatore sa che la misura non è affetta
da errori sistematici, che
lo strumento è ben calibrato e che l'indicazione è effettuata
arrotondando le cifre successive a quella indicata
secondo le regole ``delle calcolatrici tascabili'' (fino
a 4 approssima per difetto, dal 5 - compreso - in poi per eccesso).
Se lo sperimentatore legge
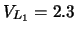 V e
V e
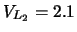 V, quanto vale la previsione (con la sua incertezza)
della differenza
fra i valori veri delle tensioni? (Si costruiscano le distribuzioni
delle variabili associate ai valori veri delle grandezze fisiche
di interesse, al centesimo di Volt, dato questo stato di informazione).
V, quanto vale la previsione (con la sua incertezza)
della differenza
fra i valori veri delle tensioni? (Si costruiscano le distribuzioni
delle variabili associate ai valori veri delle grandezze fisiche
di interesse, al centesimo di Volt, dato questo stato di informazione).
-
 Sul problema precedente. Quanto vale la probabilità che, nelle
condizioni precedentemente illustrate, nei due punti del circuito
la tensione ``vera'' sia la stessa?
Sul problema precedente. Quanto vale la probabilità che, nelle
condizioni precedentemente illustrate, nei due punti del circuito
la tensione ``vera'' sia la stessa?
-
 Vengono misurate due temperature con due termometri simili
aventi un
display digitale al grado. Si sa che quei termometri hanno
una probabilità del 70% di indicare la temperature giusta,
del 15% di indicare un grado in più e del 15% di indicare un grado
in meno. I due termometri danno informazioni indipendenti in quanto non
è stato possibile intercalibrarli. I due termometri indicano
85 e 81
Vengono misurate due temperature con due termometri simili
aventi un
display digitale al grado. Si sa che quei termometri hanno
una probabilità del 70% di indicare la temperature giusta,
del 15% di indicare un grado in più e del 15% di indicare un grado
in meno. I due termometri danno informazioni indipendenti in quanto non
è stato possibile intercalibrarli. I due termometri indicano
85 e 81 C, temperature per le quali
il giudizio a priori dello sperimentatore è
molto più vago dell'informazione fornita dallo strumento.
Cosa si può dire sulla differenza di temperatura?
C, temperature per le quali
il giudizio a priori dello sperimentatore è
molto più vago dell'informazione fornita dallo strumento.
Cosa si può dire sulla differenza di temperatura?
- Un appassionato di lotto decide di ``inseguire'' un certo
numero su una certa ruota. Quanto vale la probabilità che
egli riesca a vincere entro,
rispettivamente,
10, 18, 30, 50 e 100 estrazioni? Quanto vale la probabilità
che il numero esca alla 101-ma estrazione nei casi che
si sia verificato o che non si sia
non verificato precedenetemente?
- Una persona gioca sempre le stesse due colonne all'enalotto,
sperando che prima o poi possano uscire. Calcolare
previsione e incertezza di previsione del numero di
volte che dovrà giocare per vincere.
- pzd100
Si immagini una variabile casuale definita su un intervallo
finito, per semplicità
![$ X \in [0,1]$](img1255.png) . Mostrare che la distribuzione
di massima varianza è quella che concentra la probabilità
agli estremi dell'intervallo. Si verifichi, ad esempio,
la varianza diminuisce se: a) le probabilità dei due estremi
diventano, rispettivamente,
. Mostrare che la distribuzione
di massima varianza è quella che concentra la probabilità
agli estremi dell'intervallo. Si verifichi, ad esempio,
la varianza diminuisce se: a) le probabilità dei due estremi
diventano, rispettivamente,
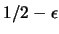 e
e
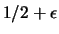 ;
b) due punti molto prossimi agli estremi
(
;
b) due punti molto prossimi agli estremi
(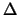 e
e 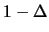 )
acquistano una probabilità
diversa da zero.
)
acquistano una probabilità
diversa da zero.
- Una variabile casuale è definita nell'intervallo compreso fra
100 e 1000. È possibile immaginare una distribuzione di probabilità
tale che la deviazione standard valga 500 o più?
- Si rianalizzi il problema 13 del capitolo 4 alla luce delle distribuzioni
di probabilità. Quanto vale la previsione (con la sua incertezza)
del tentativo in cui la pistola fa fuoco?
- In un gioco di società uno dei partecipanti è ``finito in prigione''
e può riprendere il gioco soltanto quando riuscirà ad ottenere
il numero 1 con il lancio di un dado. Quanto vale le probabilità che
ci riesca entro il terzo colpo?
- Una persona gioca alla roulette a rosso e nero
praticando la strategia di raddoppio descritta nel paragrafo
6.17, cominciando
con una puntata iniziale di
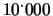 .
Calcolare la probabilità che egli perda oltre
10 milioni la prima serie di giocate (per semplificare i conti si
trascuri l'effetto dello zero).
.
Calcolare la probabilità che egli perda oltre
10 milioni la prima serie di giocate (per semplificare i conti si
trascuri l'effetto dello zero).
- Un banco di roulette accetta puntate
massime di 100 milioni. Un miliardario
comincia a giocare
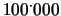 lire,
raddoppiando la puntata dopo ogni perdita.
Calcolare previsione e incertezza di previsione
di vincita tenendo conto dell'effetto dello zero.
lire,
raddoppiando la puntata dopo ogni perdita.
Calcolare previsione e incertezza di previsione
di vincita tenendo conto dell'effetto dello zero.
- Paradosso di San Pietroburgo (baclawski, pag. 174)




Next: Distribuzioni di probabilità di
Up: Variabili casuali e distribuzioni
Previous: Ricapitolando
Indice
Giulio D'Agostini
2001-04-02
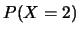 ;
;
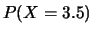 ;
;
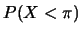 ;
;
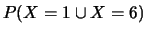 ;
;
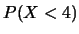 ;
;
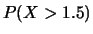 ;
;
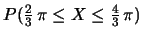 .
.