



Next: Estensione dei teoremi sulla
Up: Previsione quantitativa della distribuzione
Previous: Inferenza probabilistica su
Indice
Vediamo ora come l'incertezza su 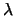 si propaga
sull'incertezza sui futuri esiti, e quindi sulla
possibile distribuzione statistica che sarà osservata.
Concentriamoci, tanto per
fare un esempio, sul valore
si propaga
sull'incertezza sui futuri esiti, e quindi sulla
possibile distribuzione statistica che sarà osservata.
Concentriamoci, tanto per
fare un esempio, sul valore 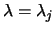 (due morti).
Subordinatamente all'ipotesi
(due morti).
Subordinatamente all'ipotesi
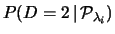 si calcola:
si calcola:
Pesando le varie ipotesi con le loro
probabilità (legge delle alternative, vedi
paragrafo 4.9.2):
Scrivendo le probabilità in termini delle funzioni di probabilità
otteniamo
L'espressione generale della distribuzione di probabilità
di 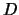 diventa:
diventa:
*** per fare le cose bene si dovrebbe introdurre la multinomiale ***




Next: Estensione dei teoremi sulla
Up: Previsione quantitativa della distribuzione
Previous: Inferenza probabilistica su
Indice
Giulio D'Agostini
2001-04-02
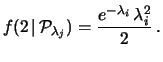
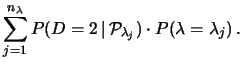
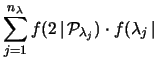
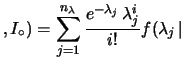 dati
dati