



Next: Vita media di decadimento
Up: Processo di Poisson -
Previous: Relazione fra esponenziale e
Indice
Considerando un processo di Poisson nel dominio del tempo
di intensità  , si può
essere, in generale, interessati alla variabile casuale
, si può
essere, in generale, interessati alla variabile casuale
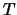 ``tempo di attesa affinché si verifichi
il
``tempo di attesa affinché si verifichi
il  -mo successo''. Il caso
-mo successo''. Il caso 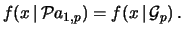 è quello descritto dall'esponenziale.
Consideriamo l'evento
è quello descritto dall'esponenziale.
Consideriamo l'evento  ``il successo
``il successo  -mo si verifica
ad un tempo
-mo si verifica
ad un tempo  ''. La richiesta di questo evento corrisponde
alla richiesta che entro il tempo
''. La richiesta di questo evento corrisponde
alla richiesta che entro il tempo  si siano verificati
al più
si siano verificati
al più 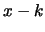 successi. Quindi, poiché il numero di successi
nel tempo
successi. Quindi, poiché il numero di successi
nel tempo  è dato da una distribuzione di Poisson di parametro
è dato da una distribuzione di Poisson di parametro
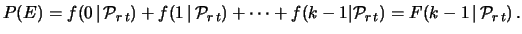 ,
abbiamo:
La probabilità che l'ennesimo successo si verifichi
entro il tempo
,
abbiamo:
La probabilità che l'ennesimo successo si verifichi
entro il tempo  è uguale a
è uguale a
Si può verificare - integrando iterativamente per parti - che
quest'ultima espressione è soluzione del seguente integrale:
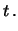
d
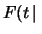
Otteniamo finalmente la funzione di partizione e quindi la distribuzione di
probabilità cercate, nota come distribuzione di Erlang:
Figura:
Distribuzione del tempo di attesa
del  -mo successo (``Erlang'') in un processo di Poisson di intensità
-mo successo (``Erlang'') in un processo di Poisson di intensità
 tale che
tale che 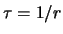 sia pari a 1 e 0.5 secondi,
con
sia pari a 1 e 0.5 secondi,
con  uguale
a 1 (--), 2 (- - - -),
3 (
uguale
a 1 (--), 2 (- - - -),
3 (
 ) e 5 (
) e 5 (
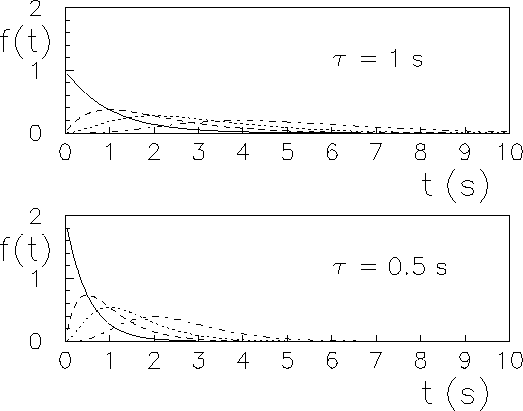 ).
).
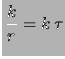 |
Valore atteso, varianza e deviazione standard valgono
rispettivamente
E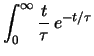 |
 |
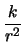 |
(8.27) |
Var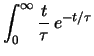 |
 |
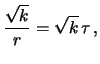 |
(8.28) |
 |
 |
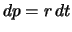 |
(8.29) |
ove si è fatto uso anche di 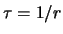 per esprimere il risultato
in modo più intuitivo: la previsione del tempo di attesa
è pari a
per esprimere il risultato
in modo più intuitivo: la previsione del tempo di attesa
è pari a  volte quello di attesa del primo
successo, mentre la deviazione standard aumenta come la radice quadrata
del numeri di successi. Valore atteso e varianza possono essere
valutati in modo molto semplice pensando a
volte quello di attesa del primo
successo, mentre la deviazione standard aumenta come la radice quadrata
del numeri di successi. Valore atteso e varianza possono essere
valutati in modo molto semplice pensando a  distribuzioni
esponenziali (vedi paragrafo 10.7).
La distribuzione di Erlang sta alla distribuzione
esponenziale come la distribuzione di Pascal sta alla geometrica.
distribuzioni
esponenziali (vedi paragrafo 10.7).
La distribuzione di Erlang sta alla distribuzione
esponenziale come la distribuzione di Pascal sta alla geometrica.
La distribuzione può essere estesa anche a valori di  non interi,
ottenendo la distribuzione Gamma (vedi par. 12.4).
non interi,
ottenendo la distribuzione Gamma (vedi par. 12.4).




Next: Vita media di decadimento
Up: Processo di Poisson -
Previous: Relazione fra esponenziale e
Indice
Giulio D'Agostini
2001-04-02
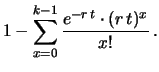
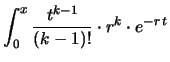
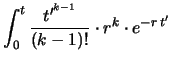
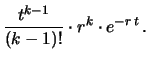 Erlang
Erlang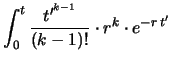
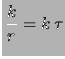
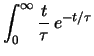
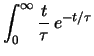
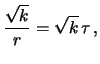

![]() non interi,
ottenendo la distribuzione Gamma (vedi par. 12.4).
non interi,
ottenendo la distribuzione Gamma (vedi par. 12.4).