



Next:
Up: Altre distribuzioni di interesse
Previous: Chi
Indice
 di Student
di Student
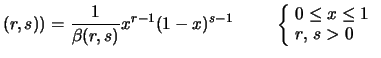 Student Student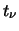 |
(8.47) |
La variabile che segue la distribuzione di Student
è indicata usualmente con il simbolo  (o
(o  )
e chiamata ``
)
e chiamata `` di Student''.
Come per il caso della distribuzione di Chi
di Student''.
Come per il caso della distribuzione di Chi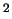 ,
il parametro
,
il parametro 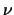 , non necessariamente intero è detto
numero di gradi di libertà.
Valore atteso e varianza sono:
, non necessariamente intero è detto
numero di gradi di libertà.
Valore atteso e varianza sono:
E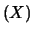 |
 |
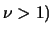 se se 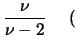 |
(8.48) |
Var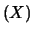 |
 |
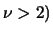 se se  |
(8.49) |
mentre la moda vale 0.
La funzione generatrice dei momenti non esiste.
Figura:
Esempi di distribuzioni di  di Student per
di Student per
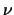 uguale a 1 (curva più larga), 2, 5, 10 e 100
(
uguale a 1 (curva più larga), 2, 5, 10 e 100
(
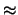 ``
``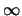 '').
'').
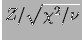 |
Una proprietà importante per l'uso è la seguente:
se si hanno una variabile 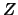 che segue una normale standardizzata
e una variabile
che segue una normale standardizzata
e una variabile
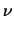 che segue una distribuzione di Chi
che segue una distribuzione di Chi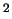 con
con 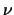 gradi di libertà e le due variabili sono indipendenti,
allora la nuova variabile
gradi di libertà e le due variabili sono indipendenti,
allora la nuova variabile
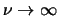 segue una distribuzione
di Student di parametro
segue una distribuzione
di Student di parametro 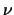 .
.
La  di Student ha una forma a campana come la gaussiana, ma con
code più pronunciate per piccoli valori di
di Student ha una forma a campana come la gaussiana, ma con
code più pronunciate per piccoli valori di 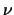 .
Per
.
Per 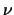 grande (virtualmente per
grande (virtualmente per
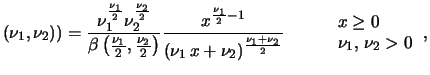 , ma in pratica
quando
, ma in pratica
quando 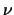 supera la decina) la distribuzione tende ad una
gaussiana standardizzata.
supera la decina) la distribuzione tende ad una
gaussiana standardizzata.




Next:
Up: Altre distribuzioni di interesse
Previous: Chi
Indice
Giulio D'Agostini
2001-04-02
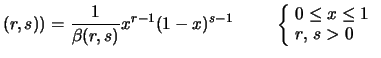 Student
Student
![]() di Student ha una forma a campana come la gaussiana, ma con
code più pronunciate per piccoli valori di
di Student ha una forma a campana come la gaussiana, ma con
code più pronunciate per piccoli valori di ![]() .
Per
.
Per ![]() grande (virtualmente per
grande (virtualmente per
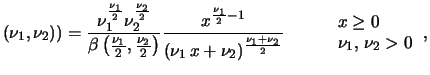 , ma in pratica
quando
, ma in pratica
quando ![]() supera la decina) la distribuzione tende ad una
gaussiana standardizzata.
supera la decina) la distribuzione tende ad una
gaussiana standardizzata.