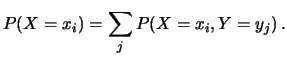Next: Distribuzioni marginali
Up: Vettori aleatori
Previous: Variabili casuali doppie discrete
Indice
Per introdurre le variabili continue partiamo
dalla funzione di ripartizione:
In questo caso l'elemento infinitesimo di probabilità è pari a:
Esso ha il significato di
La funzione densità di probabilità, ottenuta dalla
funzione di ripartizione come
rappresenta invece il grado di fiducia del punto 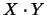 ,
come discusso al momento
di introdurre le variabili continue.
Le proprietà della densità di probabilità congiunta
,
come discusso al momento
di introdurre le variabili continue.
Le proprietà della densità di probabilità congiunta 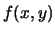 sono analoghe al caso unidimensionale visto nel capitolo precedente.
Ricordiamo soltanto che
sono analoghe al caso unidimensionale visto nel capitolo precedente.
Ricordiamo soltanto che 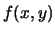 ha le dimensioni
inverse di
ha le dimensioni
inverse di 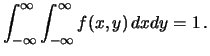 e che la condizione di
normalizzazione diventa:
e che la condizione di
normalizzazione diventa:
Giulio D'Agostini
2001-04-02
![$\displaystyle P[(x\le X \le x + dx)
\cap (y\le Y\le y+dy)]\,.$](img2173.png)
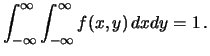 e che la condizione di
normalizzazione diventa:
e che la condizione di
normalizzazione diventa: