



Next: Trasformazione di una variabile
Up: Soluzione generale per variabili
Previous: Regola generale
Indice
Consideriamo la variabile 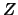 , somma di due variabili indipendenti
, somma di due variabili indipendenti  e
e
 . Applicando la regola generale otteniamo
che
. Applicando la regola generale otteniamo
che
Nel caso di variabili indipendenti la (10.8) si riduce
a
| |
 |
 |
(10.9) |
che rappresenta il
caso discreto della
convoluzione di due funzioni di probabilità indipendenti.
La figura 10.1 mostra la distribuzione della somma
di due variabili casuali uniformi associate agli esiti del lancio
di due dadi. È anche mostrata la somma di tre dadi, la quale può essere
interpretata come la somma di due dadi più un terzo dado. Si noti
l'alta probabilità dei valori centrali e la bassa probabilità
di quelli laterali.
Figura:
Distribuzione della somma dei risultati ottenuti dal lancio di
 dadi. La concentrazione della probabilità al centro della
distribuzione è dovuta all'elevato numero di combinazioni i quali
producono risultati intermedi e giustifica qualitativamente il teorema del
limite centrale.
dadi. La concentrazione della probabilità al centro della
distribuzione è dovuta all'elevato numero di combinazioni i quali
producono risultati intermedi e giustifica qualitativamente il teorema del
limite centrale.
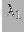 |
Come esempio di applicazione della
(10.9)
consideriamo la somma di due variabili ciascuna delle
quali è una distribuzione di Poisson, con parametri 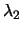 e
e
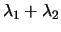 . Abbiamo già detto,
basandoci su argomenti legati all'interpretazione fisica del processo
di Poisson, che la distribuzione della somma è ancora
una poissoniana di parametro
. Abbiamo già detto,
basandoci su argomenti legati all'interpretazione fisica del processo
di Poisson, che la distribuzione della somma è ancora
una poissoniana di parametro
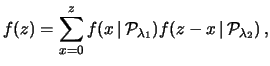 . Utilizzando la
(10.9) otteniamo:
. Utilizzando la
(10.9) otteniamo:
ove la sommatoria va da 0 a 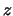 in quanto
in quanto 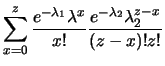 non può assumere valori
negativi. Esplicitando le funzioni si ottiene:
non può assumere valori
negativi. Esplicitando le funzioni si ottiene:
in cui l'ultimo passaggio
è dovuto al fatto che
la sommatoria è uguale allo sviluppo
del binomio




Next: Trasformazione di una variabile
Up: Soluzione generale per variabili
Previous: Regola generale
Indice
Giulio D'Agostini
2001-04-02
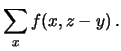
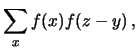
![]() e
e
![]() . Abbiamo già detto,
basandoci su argomenti legati all'interpretazione fisica del processo
di Poisson, che la distribuzione della somma è ancora
una poissoniana di parametro
. Abbiamo già detto,
basandoci su argomenti legati all'interpretazione fisica del processo
di Poisson, che la distribuzione della somma è ancora
una poissoniana di parametro
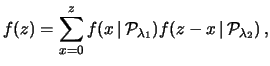 . Utilizzando la
(10.9) otteniamo:
. Utilizzando la
(10.9) otteniamo:
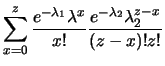 non può assumere valori
negativi. Esplicitando le funzioni si ottiene:
non può assumere valori
negativi. Esplicitando le funzioni si ottiene: