Somma di due variabili distribuite normalmente

Un caso molto interessante è quello della somma di due variabili indipendenti distribuite normalmente. Applicando la formula di convoluzione si ha

$$f(z) = \int_{-\infty}^{+\infty} \frac{1}{2\,\pi\,\sigma_X\sigma_... ...\frac{(x-\mu_X)^2}{2\,\sigma_X^2} -\frac{(z-x-\mu_Y)^2}{2\,\sigma_Y^2}\right]\,$$d$$x\,.$$

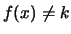
Effettuando l'integrale^10.6 si ottiene

$$f(z) = \frac{1}{\sqrt{2\,\pi}\sqrt{\sigma_X^2+\sigma_Y^2}} \exp\left[-\frac{\left[z-(\mu_X+\mu_Y)\right]^2} {2(\sigma_X^2+\sigma_Y^2)}\right]\,.$$ (10.20)

La somma è ancora distribuita normalmente con

$$\mu_Z = \mu_X+\mu_Y$$ (10.21)

$$\sigma_Z^2 = \sigma_X^2+\sigma_Y^2$$ (10.22)

Utilizzando il risultato precedente sulla trasformazione lineare di una variabile (vedi (10.15)), possiamo affermare che la combinazione lineare di variabili casuali indipendenti distribuite normalmente è ancora distribuita normalmente. In altre parole, la gaussiana gode di una proprità riproduttiva più generale di quella di cui godono binomiale e poissoniana.