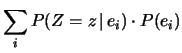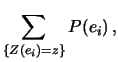- ... dadi1.1
- pzd100Questo
approccio è compatibile sia con
la corrente di pensiero che crede che la
la meccanica quantistica esaurisca la
descrizione del mondo fisico sia con quella che
protende per le famose ``variabili nascoste'', secondo la visione
di Einstein.
Questo concetto è stato espresso molto chiaramente già nel 1748
da Hume, il quale, pur credendo che le leggi della natura dovessero
essere deterministiche, affermava:
``Per quanto non vi sia nel mondo qualche cosa come il Caso,
la nostra ignoranza della causa reale di ogni evento ha la
stessa influenza sull'intelletto e genera una simile specie di
credenza''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
semplicit\`a1.2
- Si vedrà come queste postille di
subordinazione delle conclusioni scientifiche a conoscenze e
``pregiudizi'' a priori giocano un ruolo fondamentale nei
processi di misura e di accettazione di teorie da parte della
comunità scientifica.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
arbitraria1.3
- Ma dopo l'osservazione della prima sequenza mostrata
aumenta il sospetto
che si tratti di una moneta con due teste, qualora
ci siano delle buone ragioni per far sorgere un simile dubbio.
Il concetto di probabilità servirà a quantificare
il grado di tale sospetto.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... secolo,1.4
- L'interesse alla stima
quantitativa dell'incertezza di misura può essere fatto risalire
al lavoro di Laplace e Gauss, all'inizio del 1800.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
l'aggiornamento1.5
- Ma anche in questo caso si è imparato
qualcosa, cioè che il termometro non funziona...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... falso1.6
- pzd100Questa
schematizzazione segue lo
schema tradizionale della logica dicotomica, di origine aristotelica
e universalmente diffusa,
in cui un evento può essere soltanto vero o falso. La descrizione
del mondo reale è più complicata e un evento può essere
in parte vero in parte falso. Si pensi ad affermazioni del
tipo ``persona alta'',
``ragazza carina'', ``uomo sportivo'', o anche
``piove a Roma''. Citando un esempio classico, ``quale
sasso è responsabile della transizione da non-mucchio
a mucchio?''.
Da alcuni decenni si è sviluppata la cosiddetta
fuzzy logic - logica sfumata - che si avvicina meglio
di quella tradizionale al modo di classificazione del cervello umano.
Nel seguito non ci interesseremo di questo tipo di logica, sia
per il carattere introduttivo del corso, sia perché la maggior
parte degli eventi dei quali ci occuperemo si prestano abbastanza bene
ad una classificazione di tipo dicotomico
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
cultura1.7
- pzd100Si badi bene che le cose
cambiano molto se si prendono in considerazione eventi più complicati
e che in genere richiedono dei conti anche ad esperti. Così pure - come è ben noto - l'intuizione di molti può
essere tratta in inganno quando si chiede
quale faccia esce
dopo che si sono verificate 5 teste. Quindi bisogna stare attenti
a non fare del ``populismo probabilistico''.
Come diceva Bruno de Finetti,
per conoscere il risultato di una
certa operazione aritmetica non lo si chiede alla gente e poi si prende
un risultato medio, ma ci si
preoccuperà di insegnare loro la matematica.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Sufficiente2.1
-
Come contrapposizione al
principio di ragion sufficiente di Leibnitz,
secondo il quale ``nulla accade senza che vi sia ragione perché
accada proprio così invece che altrimenti''
(una versione più raffinata del popolare
``non muove foglia che Dio non voglia'').
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Poincar\'e2.2
- Henry Poincaré, ``Scienza e Ipotesi''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... futuro2.3
- pzd100Questo
processo dell'intelletto umano è descritto molto bene da
Hume nel capitolo ``Probabilità''
del suo ``Saggio sull'intelletto umano":
``Essendo costretti dalla consuetudine a trasferire il passato
al futuro in tutte le nostre inferenze, quando il passato
si è manifestato del tutto regolare e uniforme ci aspettiamo
un evento con la massima sicurezza e non lasciamo posto a qualche altra
supposizione contraria. ...Sebbene diamo la preferenza a quello
che è stato trovato più usuale e crediamo che questo effetto
si verificherà, non dobbiamo trascurare gli altri effetti, ma dobbiamo
assegnare a ciascuno di essi un particolare peso e autorità
in proporzione a come lo abbiamo trovato più o meno frequente''.
Francamente, mi sembra fra le cose più sensate
dette a giustificazione dell'uso della frequenza di eventi passati
come valutazione della probabilità di eventi futuri.
Questa semplice constatazione
è senz'altro più convincente dei tentativi di far discendere
tale prassi dalla ``Legge empirica del Caso'',
dal paradossale uso del teorema di Bernoulli a tale scopo
(vedi nota nel seguito), o
dai macchinosi tentativi di matematizzazione attraverso i ``collettivi'' di
von Mises.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... misurare2.4
- La
determinazione dei valori
delle costanti fondamentali è soltanto uno dei tanti aspetti della
problematica della misura.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... caso2.5
- pzd100In molti testi il ruolo
di anello di congiunzione fra le due ``definizioni''
è affidato al Teorema di Bernoulli, che vedremo nel seguito.
Anticipiamo che esso afferma che, al ``crescere del numero di prove,
diventa piccola a piacere
la probabilità che la frequenza relativa differisca dalla
probabilità dell'evento favorevole in ciascuna delle prove''.
Preferiamo basarci invece sulle osservazioni empiriche che hanno
condotto alla legge empirica del caso
sia perché
ci sembra più corrispondente al processo storico
che per la palese illogicità dell'uso
di questo teorema per questo scopo in quanto,
come afferma de Finetti (1970),
``non si sfugge al dilemma che la stessa cosa non
si può assumere prima per definizione e poi dimostrare come teorema,
né alla contraddizione di una definizione che
assumerebbe una cosa certa mentre il teorema
afferma che è soltanto molto probabile''.
Torneremo su queste osservazioni
nel momento appropriato.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... facce2.6
- Qualcuno ha stimato
che l'effetto dei forellini sulle facce dei dadi sia tale
che le probabilità dei valori da 1 a 6
siano da ritenersi,rispettivamente, 0.155, 0.159, 0.164,
0.169, 0.174, 0.179 (vedi Shafer, 1976).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dado2.7
- Per esempio, da misure effettuate da studenti di laboratorio,
risulta che il contributo maggiore alla non equiprobabilità
delle facce dei dadi è dovuto al fatto che i dadi commerciali non sono
cubi perfetti. Ne segue che le faccie opposte che sono più vicine fra loro
tendono ad uscire più frequentemente.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... complemento2.8
- Si
ricorda che nei dadi la somma delle facce
opposte dà 7.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ``ovvia''2.9
- La come è ben noto a chi ha avuto
cattive esperienze con compagnie di assicurazioni, quello che sembrava
ovvio è contraddetto da una delle clausole scritte a caratteri
microscopici nel contratto di assicurazioni.
I contratti di assicurazioni, infatti,
non sono altro che scommesse su eventi condizionati
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
soggettiva2.10
- R. Scozzafava, ``Probabilità soggettiva -
significato, valutazione, applicazioni'', Masson,1997
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
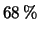 2.11
2.11
- Vedremo che in molti casi
questo sarà il modo standard di presentare i risultati
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
lineare2.12
- Questo è la ragione per cui facciamo polizze
assicurative con le quali scarichiamo grandi rischi di piccolissima
probabilità a chi è più coperto finanziariamente (che siccome
non fa di certo scommesse eque ci guadagna nel cautelare i clienti
da improbabili rovine).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Roulette2.13
- Si ricorda che alla roulette
ci sono 37 numeri, 1-36 più lo zero. Dei numeri da 1 a 36 la
metà sono rossi e la metà neri (senza un ordine semplice).
Lo zero
è un numero particolare considerato né
pari né dispari, né rosso né nero. Se si gioca puntando
sui pari o
sui dispari, o sul colore si vince una somma totale che è il doppio della
puntata, ovvero la vincita netta è pari alla puntata stessa. Se si punta
su un numero singolo si vince globalmente 36 volte la puntata.
Sono anche possibili molte
altre combinazioni di gioco sulle quali non ci possiamo soffermare. Si ricorda
inoltre che esistono al mondo altre versioni di roulette.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
puntate2.14
- L'estratto semplice è pagato 11.232 volte
la puntata, meno il 3%.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... all'enalotto2.15
-
Si ricorda che la colonna vincente dell'enalotto
è ottenuta da 12 estrazione di numeri del lotto,
assegnando i simboli ``1'', ``X'' e ``2''
a seconda che i numeri usciti siano
compresi rispettivamente fra 1 e 30, fra 31 e 60
e fra 61 e 90.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
logaritmi3.1
- Il simbolo
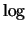 indica il logaritmo
decimale (a volte si incontra
indica il logaritmo
decimale (a volte si incontra 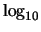 ).
Il logaritmo naturale verrà indicato con
).
Il logaritmo naturale verrà indicato con  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... scommessa4.1
- Ad esempio, il testo della legge che regola il
gioco del lotto specifica: ``Quando le matrici
rivelano incompletezza di dati o le scommesse sono state
accettate in violazione delle disposizioni dell'articolo 3 o i dati non
sono pervenuti al centro di elaborazione, le scommesse si considerano
non avvenute e il giocatore escluso dalla partecipazione all'estrazione
ha diritto al rimborso dell'importo della scommessa previa esibizione dello
scontrino al raccoglitore''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... regole4.2
- pzd100Al fine
di smitizzare il pur storicamente importante approccio assiomatico
preferiamo parlare semplicemente di ``regole'', che ovviamente
corrispondono agli assiomi. Gli assiomi 1 e 2 sono spesso presentati
nelle forme
come
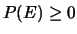 e
e
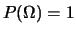 , le quali ovviamente lasciano invariate
tutte le proprietà che ne discendono.
, le quali ovviamente lasciano invariate
tutte le proprietà che ne discendono.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
numero4.3
- pzd100L'estensione dell'unione a infiniti eventi
è delicata e controversa, ma inessenziale per la nostra
trattazione.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
numero4.4
- Il simbolo ``
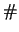 '' sta per ``numero''.
'' sta per ``numero''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... direttamente4.5
- I masochisti possono anche usare
la 4.17, che in questo caso è applicabile...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... quotidiano4.6
- La Repubblica, sabato 11/9/1993.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
tecniche4.7
- Spesso si incontrano in altre pubblicazioni
anche
elementi scaramantici, legati all'alternanza dei segni o
ai segni precedentemente usciti.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
come5.1
- Il condizionamento multiplo dell'evento
 dalle ipotesi
dalle ipotesi 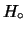 e
e 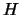 può essere indicato con
può essere indicato con
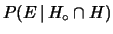 o più semplicemente con
o più semplicemente con
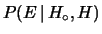 . Quando
. Quando 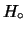 è una ipotesi di base e di cui non si ha alcun
interesse di effettuare un inversione di
probabilità si può scrivere anche
è una ipotesi di base e di cui non si ha alcun
interesse di effettuare un inversione di
probabilità si può scrivere anche
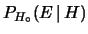 ,
,
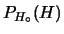 e
e
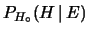 , da cui segue che
, da cui segue che
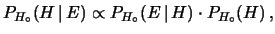 |
(5.7) |
ovvero
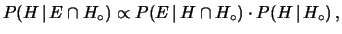 |
(5.8) |
o anche
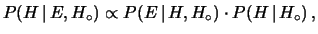 |
(5.9) |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... calcolarsi5.2
- Si noti che
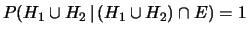 se
se
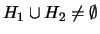 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... darebbe5.3
- Si noti che
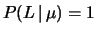 non implica assolutamente
non implica assolutamente
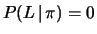 in quanto esse sono probabilità
di
in quanto esse sono probabilità
di 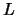 relative a diversi stati di informazione.
relative a diversi stati di informazione.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
convenire5.4
- pzd100In
realtà non è difficile convincersi che
anche in quei casi, di veramente oggettivo, nel senso che le
conclusioni seguano necessariamente
dalle osservazioni, c'è ben poco.
Riprendiamo il caso di
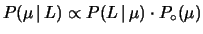 . Si può immaginare
. Si può immaginare
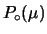 stimata dalle frequenze relative mediante un rivelatore ``perfetto'',
il quale era stato testato precedentemente
con un fascio ``puro'' di particelle
stimata dalle frequenze relative mediante un rivelatore ``perfetto'',
il quale era stato testato precedentemente
con un fascio ``puro'' di particelle
 , etc. etc. L'inesistenza nella pratica di tali stati di
preparazione sperimentale inficia ogni tentativo di passare
in modo univoco dalle osservazioni alle conclusioni. Il motivo
per il quale ciononostante tali conclusioni vengono considerate
``oggettive'' è che ``è molto improbabile incontrare
una persona ragionevole e con cognizione
di causa dei problemi di sperimentazione
che non si dichiari d'accordo che quella procedura sia corretta''.
Siamo quindi di fronte a un caso di ``intersoggettività assoluta''.
, etc. etc. L'inesistenza nella pratica di tali stati di
preparazione sperimentale inficia ogni tentativo di passare
in modo univoco dalle osservazioni alle conclusioni. Il motivo
per il quale ciononostante tali conclusioni vengono considerate
``oggettive'' è che ``è molto improbabile incontrare
una persona ragionevole e con cognizione
di causa dei problemi di sperimentazione
che non si dichiari d'accordo che quella procedura sia corretta''.
Siamo quindi di fronte a un caso di ``intersoggettività assoluta''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... iniziale5.5
- Questo si vede bene dalla (5.13).
Ad essere precisi, si può ottenere
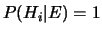 anche quando
anche quando
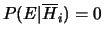 , ovvero quando le osservazioni sono incompatibili
con tutte le ipotesi alternative ad
, ovvero quando le osservazioni sono incompatibili
con tutte le ipotesi alternative ad 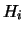 prese in considerazione (e non tutte quelle
possibili, comprese quelle formulabili nel futuro). Detto in altre
parole, in questo caso l'esperimento falsifica tutte le ipotesi
complementari formulate fino a quel momento.
Quindi una teoria può
in effetti
assumere un valore ``certezza provvisoria'' se è la sola, fra
quelle formulate, in grado di spiegare le osservazioni sperimentali.
prese in considerazione (e non tutte quelle
possibili, comprese quelle formulabili nel futuro). Detto in altre
parole, in questo caso l'esperimento falsifica tutte le ipotesi
complementari formulate fino a quel momento.
Quindi una teoria può
in effetti
assumere un valore ``certezza provvisoria'' se è la sola, fra
quelle formulate, in grado di spiegare le osservazioni sperimentali.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
scientifica5.6
- pzd100 Se
ad ogni passo dello sviluppo delle idee scientifiche
ci si fosse dovuti attenere solo alle ipotesi certe ...non ci sarebbe stato
progresso scientifico, ma una situazione di stallo. La comunità scientifica
per fortuna si muove mediamente nella direzione che sembra più credibile,
con i successi e gli inevitabili insuccessi che le decisione in
stato di incertezza comportano.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
credo5.7
- Un punto di vista alternativo è quello di rinunciare
a dare un valore di realtà alle ipotesi fisiche (e quindi anche
ai ``valori veri'' di grandezze fisiche,
per quanto detto nel capitolo 1).
Questo punto di vista
è espresso molto bene da de Finetti:
``E illusorio attribuire a una teoria o a una legge un significato
apodittico ma tuttavia esiste chiaramente un significato
pragmatico in quanto essa induce ad attendere che certi fatti
si svolgano nel modo
che noi riteniamo conforme all'idea che di tale teoria o legge
ci siamo fatti. La formulazione di una teoria, di una legge,
è un anello - in certa misura infido perché metafisico ma tuttavia
spesso necessario come tentativo di sintesi semplificativa di cose complesse
- del processo mentale per cui passiamo dall'osservazione di fatti passati
alla previsione di fatti futuri. In definitiva è solo dei
fatti, dei singoli fatti, che ha senso parlare. È ai fatti, che
(se sono futuri, e se comunque ne ignoriamo l'esito)
possiamo attribuire una probabilità''.
Detto in parole povere, si tratta di convenire se la predittività
delle leggi fisiche sia da intendersi rispetto ad osservazioni
future o rispetto a intangibili ``valori veri''.
Schematizzando nei processi di misura ai quali siamo interessati,
questo vorrebbe dire che non ha senso
parlare della probabilità che il valore vero
di una grandezza fisica sia in un certo intervallo, subordinatamente
alle osservazioni sperimentali. Sarebbe rilevante parlare soltanto
della probabilità che, in un esperimento
futuro, l'indicazione dello strumento
cada in un certo intervallo, subordinatamente alle osservazioni
precedenti
e alla conoscenza delle condizioni di tale esperimento.
Anche se questo punto di visto sembra più realista di quello dell'estensione
del concetto di evento illustrato nel testo,
è innegabile il vantaggio pratico di considerare i valori
di grandezze fisiche alla stessa stregua degli eventi reali.
Per questo motivo la teoria dell'incertezza di misura che
sarà sviluppata nella terza parte del testo
si baserà su tale approccio e sull'ipotesi di esistenza
di ``valori veri'' di grandezze fisiche.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fornitore5.8
- Questo tipo di strumenti, che sembrano
una vera assurdità per misure di routine, vogliono essere,
``mutatis mutandis'',
una metafora di quanto avviene comunemente
nella ricerca avanzata.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... aleatorio6.1
- Questo è forse il nome che rende meglio
l'idea. In questo testo si è preferito utilizzare come
nome standard ``variabile casuale'' in quanto è la denominazione
più usuale fra i fisici. Esso però rischia di prestarsi
ad interpretazione troppo legate ai risultati di esperimenti
ripetuti e non, più in generale, allo stato di incertezza.
Cercheremo comunque di usare i due termini come sinonimi, insistendo
su ``numero aleatorio'', o `numero incerto''..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... valori6.2
- In altri testi
le variabili discrete che assumono valori interi vengono
di preferenza
indicate con
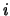 ,
, 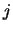 ,
,  o
o  , mentre la lettera
, mentre la lettera  è usata solo per variabili continue. In questo testo viene
generalmente
usato lo stesso simbolo
è usata solo per variabili continue. In questo testo viene
generalmente
usato lo stesso simbolo  sia per variabili discrete che continue.
sia per variabili discrete che continue.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... valori6.3
- Si noti quindi che discreto non significa
necessariamente valore intero, anche se questo sarà il caso
più frequente nelle applicazioni semplici che tratteremo.
Ad esempio, se si associa ad ogni faccia del dado la variabile
casuale
 = ``radice quadrata del numero impreso sulla faccia'',
si ottiene una variabile discreta a valori reali.
= ``radice quadrata del numero impreso sulla faccia'',
si ottiene una variabile discreta a valori reali.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
indicare6.4
- In altri testi si preferisce
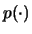 a
a 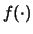 ,
a ricordare che essa ha il significato di probabilità.
Altre volte ancora si trova, ad esempio,
,
a ricordare che essa ha il significato di probabilità.
Altre volte ancora si trova, ad esempio, 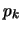 al posto di
al posto di 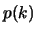 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... seguenti6.5
- Dal punto di vista formale,
la probabilità, per esempio, di
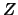 è valutata
dalla legge delle alternative (cfr. par. 4.9.2):
è valutata
dalla legge delle alternative (cfr. par. 4.9.2):
ovvero la somma delle probabilità di tutti gli eventi
di una classe completa per i quali la variabile 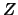 vale
vale 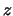 .
Il passaggio dalla (6.3) alla (6.3)
si basa sul fatto che essendo la regola di costruzione della variabile
casuale univoca,
.
Il passaggio dalla (6.3) alla (6.3)
si basa sul fatto che essendo la regola di costruzione della variabile
casuale univoca,
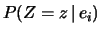 può valere soltanto 0 o 1.
può valere soltanto 0 o 1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... definita6.6
- Ad esempio, nel caso
del valore ottenuto nel lancio di un dado,
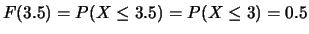 .
Anche se a qualcuno potrà sembrare strano che ci si possa interessare
di
.
Anche se a qualcuno potrà sembrare strano che ci si possa interessare
di
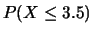 nel lancio dei dadi è fuori
di dubbio l'espressione probabilistica sia corretta, come lo sarebbe
nel lancio dei dadi è fuori
di dubbio l'espressione probabilistica sia corretta, come lo sarebbe
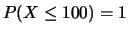 o
o 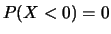 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
tipo''6.7
- Ma non è corretto parlare dello stesso evento.
Infatti, ogni evento, come affermazione sul verificarsi di un qualche
accadimento è unico e irripetibile. Quindi se si lancia 100 volte una moneta
si possono considerare gli eventi ``testa al primo lancio'',
``testa all'
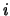 -mo lancio'', ``nessuna
testa nei primi 5 lanci'', eccetera, ma non ``l'evento testa''.
-mo lancio'', ``nessuna
testa nei primi 5 lanci'', eccetera, ma non ``l'evento testa''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... che6.8
- pzd100Questa definizione
del concetto di incertezza è ottenuta
parafrasando la definizione ISO di incertezza di misura (vedi anche
paragrafo 2.11.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... probabilit\`a6.9
- Si noti il diverso uso delle
lettere maiuscole e minuscole, consistenti con le definizioni
introdotte.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... aleatori6.10
- pzd100Si noti che la
richiesta di previsione nulla
in caso di valutazioni coerenti di probabilità è valida soltanto se
i numeri casuali hanno il significato di guadagni netti
(con segno) associati
ad ogni scommessa. Ad esempio, scommettendo alla pari 1000 lire
nel lancio di una moneta, la previsione di guadagno è nulla, mentre,
associando all'evento testa il valore
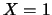 e all'evento croce
e all'evento croce
 , la previsione della variabile casuale
, la previsione della variabile casuale  è 1/2.
è 1/2.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
evento6.11
- pzd100Questa scelta è motivata
dal fatto che il simbolo
E
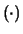 è quello più largamente
usato nella letteratura scientifica.
Tuttavia preferiamo usare
il termine ``previsione'' per designarlo,
in quanto è quello che rende meglio
l'idea del concetto (questo risulterà più chiaro quando ad esso
sarà affiancato il concetto di ``incertezza di previsione'').
è quello più largamente
usato nella letteratura scientifica.
Tuttavia preferiamo usare
il termine ``previsione'' per designarlo,
in quanto è quello che rende meglio
l'idea del concetto (questo risulterà più chiaro quando ad esso
sarà affiancato il concetto di ``incertezza di previsione'').
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... genere6.12
- Un controesempio è
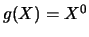 , nota con certezza
se
, nota con certezza
se 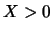 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
uguale6.13
- Si presti attenzione al fatto che, se la funzione
non è monotona e sia
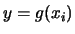 , non vuol dire che, in generale,
, non vuol dire che, in generale,
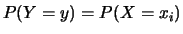 . Infatti, bisogna sommare le probabilità di
tutti i valori di
. Infatti, bisogna sommare le probabilità di
tutti i valori di  per i quali g(X)=y. Ma questo è
un altro argomento e verrà trattato nel capitolo 10.
Le formule che seguono sono
valide anche nel caso di funzioni non monotone.
per i quali g(X)=y. Ma questo è
un altro argomento e verrà trattato nel capitolo 10.
Le formule che seguono sono
valide anche nel caso di funzioni non monotone.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
stessa6.14
- Si noti come si considerino gli scarti previsti
e non quelli osservati.
Insistiamo nel ripetere che l'incertezza di previsione,
così come la probabilità, è un concetto che si applica
sui numeri rispetto ai quali si è in stato di incertezza e non
ai numeri che si sono verificati. A questi è associato invece il
concetto di distribuzione statistica, come già
indicato nel paragrafo
6.3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
strategia6.15
- Si ricorda che la
ragione profonda dell'errore consiste nel ``dimenticare''
- o più propriamente nel rifiutarsi
di credere -
all'equiprobabilità delle singole prove, espresso anche con
l``assenza di memoria'' della distribuzione geometrica
(vedi paragrafo 8.12.3).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... settore6.16
- ``Il manuale del lotto'',
Mariotti Publishing, Milano, 1996.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... netto'',6.17
- Con l'aiuto di un tabaccaio,
è stato possibile accertarsi che per ogni lira giocata si ricevono
11.235 lire, ovvero si vince 10.235 volte quanto viene puntato.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... campionaria6.18
- Qualcuno vorrebbe
anche separare i concetti mediante i termini media e
valore medio, ma mi sembra una battaglia persa, in quanto
intuitivamente essi non fanno riferimento a cose diverse.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... atteso7.1
- In
particolare, non è vero che ``il numero di
teste tende al numero di croci'', come si sente dire
talvolta. Questa affermazione, oltre
che essere assolutamente fuorviante quando si
pensa ad un effetto di ``recupero'' di un esito sull'altro per
``mantenersi in pari'',
è anche errata quando si pensa ad una previsione di piccoli scarti
fra i due esiti. Questo discorso sarà ripreso quando
si parlerà delle cattive interpretazioni
della legge dei grandi numeri.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Indichiamo7.2
- Lo si potrebbe anche chiamare
 , avendo esso il significato di valore atteso, e così
si trova difatti in alcuni testi. Qui preferiamo dare un simbolo proprio
al parametro della poissoniana.
, avendo esso il significato di valore atteso, e così
si trova difatti in alcuni testi. Qui preferiamo dare un simbolo proprio
al parametro della poissoniana.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
distribuzione,7.3
- *** Mettere in nota? ***
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
regolari7.4
- Si faccia attenzione ai diversi simboli
per le varie binomiali che entrano in gioco.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
passato7.5
- Si noti il salto logico rispetto alla
semplice valutazione
della probabilità dalla frequenza di ciascuna classe di eventi,
ovvero, la probabilità di
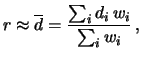 , ad esempio,
non è valutata dalla frequenza di zero morti nel passato.
Quindi, anche se si stanno utilizzando informazioni statistiche
la probabilità non è valutata secondo il paradigma frequentista.
, ad esempio,
non è valutata dalla frequenza di zero morti nel passato.
Quindi, anche se si stanno utilizzando informazioni statistiche
la probabilità non è valutata secondo il paradigma frequentista.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ``verifica''7.6
- Come dicevamo nel primo capitolo,
la natura probabilistica di tali leggi preclude ogni vericabilità
oggettiva. Sono i nostri pregiudizi sulla regolarità delle leggi
della natura a convincerci che ragionevolmente il processo
si sia svolto in quel modo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
reggimento7.7
- Si noti l'importanza di considerare
un altro reggimento, invece di estrarre a
caso uno dei duecento
dai quali è stata ricavata
la distribuzione statistica. In questo caso la probabilità
è data dal numero dei ``casi'' favorevoli (22) diviso il numero dei casi
possibili (200) (si pensi all'estrazione
di uno dei duecento resoconti dei reggimenti,
ciascuno indicante il numero di morti da calcio di cavallo).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... standard8.1
- I matematici
preferiscono considerare come secondo parametro la varianza invece
della deviazione standard. Anche se in principio la
scelta è equivalente, bisogna fare attenzione ad interpretare
correttamente notazioni sintetiche del tipo
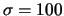 . In questo testo utilizziamo la deviazione standard
(e quindi la notazione precedente stava a significare
. In questo testo utilizziamo la deviazione standard
(e quindi la notazione precedente stava a significare
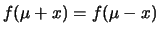 )
in quanto omogenea alla grandezza di interessa e legata al concetto
di incertezza standard di previsione.
)
in quanto omogenea alla grandezza di interessa e legata al concetto
di incertezza standard di previsione.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
standard8.2
- Come giustificazione intuitiva si pensi che:
dovendo essere costante l'area sotto la curva, al diminuire di
 deve aumentare il massimo;
deve aumentare il massimo; 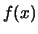 ha le dimensioni
inverse di
ha le dimensioni
inverse di  e quindi il suo denominatore deve dipendere
linearmente da
e quindi il suo denominatore deve dipendere
linearmente da  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
ripartizione8.3
- A volte la funzione di
ripartizione della normale è indicata con
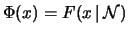 ,
ovvero:
.
,
ovvero:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... come8.4
- Questo integrale è legato alla funzione matematica
``erf(
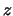 )'', il cui nome ricorda ``error function'', definita come
)'', il cui nome ricorda ``error function'', definita come
erf
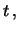
d
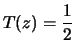

erf
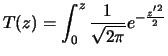
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...``evento''8.5
- Si faccia attenzione al diverso
significato che acquista qui il termine ``evento''. Secondo
la prassi scientifica esso è anche utilizzato con l'accezione
di ``occorrenza'' (ad esempio, ``l'esperimento ha registrato
1000 eventi di interazione da neutrino''). È opportuno abituarsi
a convivere a queste ambiguità di linguaggio, quando dal
contesto si evince il significato corretto del termine.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nucleoni8.6
- I neutroni hanno una
vita media di circa 20 minuti quando sono liberi (ovvero non all'interno
di un nucleo) e decadono in protone, elettrone e (anti-)neutrino.
Questo è solo modo di decadimento osservato. Altri tipi di processi
legati a nuove teorie unificatrici delle forze fondamentali,
permetterebbero sia al protone e al neutrone di decadere -
anche all'interno dei nuclei - in modi più complessi,
ma con vite medie non inferiori a
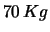 volte di quelle
supposte in questo eserzio.
volte di quelle
supposte in questo eserzio.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
\`e9.1
-
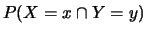 sta per
sta per
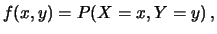 .
Si ricordi inoltre quanto detto nel capitolo
6
sulla flessibilità dell'uso di simboli.
.
Si ricordi inoltre quanto detto nel capitolo
6
sulla flessibilità dell'uso di simboli.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
ha9.2
- Chiaramente
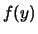 e
e 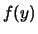 sono in genere funzioni
diverse, anche se entrambe indicate con lo stesso simbolo
sono in genere funzioni
diverse, anche se entrambe indicate con lo stesso simbolo 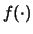 ,
cambiando solo la variabile nell'argomento. A volte, per ricordare
che si tratta di funzioni diverse, si
,
cambiando solo la variabile nell'argomento. A volte, per ricordare
che si tratta di funzioni diverse, si
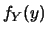 e
e 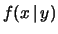 . In modo analogo dovremmo indicare
. In modo analogo dovremmo indicare
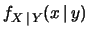 con
con
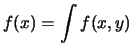 , e così via.
Eviteremo questo modo più preciso (e pesante)
in quanto non ci sono ragioni per temere ambiguità. Allo stesso
modo gli estremi degli integrali saranno omessi a sottintendere
che essi si estendono su tutti i possibili valori di
, e così via.
Eviteremo questo modo più preciso (e pesante)
in quanto non ci sono ragioni per temere ambiguità. Allo stesso
modo gli estremi degli integrali saranno omessi a sottintendere
che essi si estendono su tutti i possibili valori di  :
:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
adeguata9.3
- Per un altro modo di capire come mai la
covarianza definita come (9.16) tenda a comparire
nella teoria della probabilità si veda
la (10.27) a proposito della somma di variabili casuali.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... elementari9.4
- Si ricorda
che la lettera minuscola di
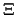 è
è 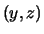 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... piccole9.5
- È da notare che il caso
in cui la formula non funziona (
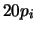 ) è quello in cui un solo
una sola modalità è certa e le altre sono impossibili e quindi
non ha più senso parlare di distribuzione di probabilità
) è quello in cui un solo
una sola modalità è certa e le altre sono impossibili e quindi
non ha più senso parlare di distribuzione di probabilità
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... integrando9.6
- Per i
calcoli si usi l'integrale indefinito:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... inversa9.7
-
Si ricorda che
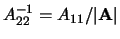 ,
,
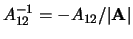 ,
,
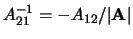 e
e
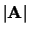 ,
dove
,
dove 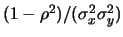 è il determinante della
matrice, il quale vale nel nostro caso
è il determinante della
matrice, il quale vale nel nostro caso
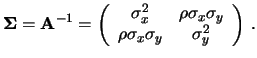 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... valori10.1
- Si noti l'uso della stessa lettera sia
per il nome della variabile che per i possibili valori.
Quando si passa alle applicazioni può essere più importante
usare gli stessi simboli sia per le grandezze che per le possibili
realizzazioni. Quindi si raccomanda di abituarsi ad una certa flessibilità.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... calibrato10.2
- Ritorneremo in dettaglio su
tale effetto (vedi paragrafo 11.6)
, ma si capisce che, ad esempio, se la misura sottostima
 sottostimerà anche
sottostimerà anche 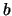 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... probabilit\`a:10.3
- Dal punto di vista formale,
la (10.5) equivale, per variabili a valori
interi (ricordiamo che discreto non implica
necessariamente intero) a
ove
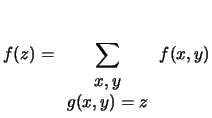 è la delta di Kronecker che vale 1 se
è la delta di Kronecker che vale 1 se 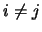 e
zero altrimenti.
e
zero altrimenti.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... diradano10.4
- Si noti che la
differenza fra il quadrato di un intero
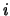 e quello
dell'intero precedente è pari a
e quello
dell'intero precedente è pari a 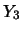 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
semplice10.5
- Un modo concettualmente semplice, analogo
al caso generale delle variabili discrete, consiste nel ``sommare''
tutti gli infiniti elementi di probabilità che danno luogo allo stesso
valore della variabile finale. Quindi, l'estensione al continuo
della forma della nota 10.2.1 è
ove
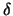 sta per la
sta per la 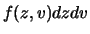 di
Dirac. Chi è familiare con questa ``funzione speciale''
può trovare di agevole impostare i conti in questo modo e,
facendo uso delle sue proprietà, ricavare facilmente le formule
che incontreremo nel seguito.
di
Dirac. Chi è familiare con questa ``funzione speciale''
può trovare di agevole impostare i conti in questo modo e,
facendo uso delle sue proprietà, ricavare facilmente le formule
che incontreremo nel seguito.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... l'integrale10.6
- Può far comodo, ad un certo punto,
l'uso del seguente integrale indefinito:
![$\displaystyle \int_{-\infty}^{+\infty}\exp\left[bx-\frac{x^2}{a^2}\right]\,$](img2737.png)
d
![$\displaystyle x
= \sqrt{a^2\pi}\exp\left[\frac{a^2b^2}{4}\right]\,.$](img2738.png)
Per il resto serve solo molta attenzione nei passaggi.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... normalmente.10.7
- Facciamo notare
come la proprietà 3) del paragrafo 8.14,
presentata in anticipo rispetto alle variabili multiple e
che riportiamo per comodità
segue dal valore atteso di 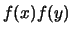 sulla funzione congiunta
sulla funzione congiunta
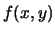 , che si riduce a
, che si riduce a 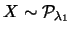 in quanto
in quanto  e
e  indipendenti.
indipendenti.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... lineare10.8
- Siccome questa notazione presenta a volte
difficoltà di interpretazione, facciamo un esempio nel caso di 2
variabili. La sommatoria
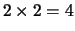 indica che bisogna considerare
le
indica che bisogna considerare
le
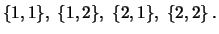 possibili combinazioni:
Quindi:
possibili combinazioni:
Quindi:
(ricordiamo che
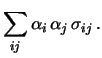 ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
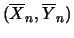 10.9
10.9
- Le variabili
 e
e  con
con  non sono invece correlate in quanto, per dirlo in
modo semplice, appartengono a diversi esperimenti. Ad esempio,
la conoscenza del valore di
non sono invece correlate in quanto, per dirlo in
modo semplice, appartengono a diversi esperimenti. Ad esempio,
la conoscenza del valore di  della prima prova non
modifica il grado di fiducia dei valori di
della prima prova non
modifica il grado di fiducia dei valori di  che possono accadere nella seconda prova.
che possono accadere nella seconda prova.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fraintesa10.10
- Un volta una
persona mi confidò:
``non credo al calcolo delle probabilità, perché mi sembra
una grande stupidaggine che se un numero non è uscito
da molte settimane debba avere più probabilità degli altri
di uscire''...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
probabilit\`a10.11
- Si ricorda
che la previsione di una distribuzione statistica
è uguale alla distribuzione di probabilità, con una incertezza
che decresce con il numero di estrazioni.
Per l'uso delle simulazioni per stimare distribuzioni
di probabilità si veda il paragrafo
10.5
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dell'articolo10.12
-
Albert Einstein, ``Opere scelte'', Bollati Boringhieri editore,
Torino 1988, pag. 136
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Galton''10.13
- È quello che gli studenti romani
chiamano familiarmente ``Pallinometro'', composto da una tavola
con chiodi disposti a ``quinconce'' fra i quali scende un pallina.
Per averne un'idea, si immagini di ruotare la
figura 10.8 di 90 gradi in senso orario, immaginando
i puntini come chiodi e il punto 0 il punto di immisione della pallina.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... `dati'.11.1
- Come discuteremo nel seguito esiste
una corrente di pensiero, fortunatamente in declino fra coloro
che si occupano dei fondamenti dell'inferenza statistica, ma tuttora
in auge per quanto riguarda le applicazioni, la quale nega che si possa
parlare di probabilità dei valori veri. Questo è il motivo per cui
si sente ancora parlare di ``incertezza dei dati'', una vera assurdità
che fa pensare che si può essere in stato di incertezza di fronte
al numero letto sul display di uno strumento. L'incertezza è
invece sul valore della grandezza che con quello strumento si vuole
misurare, ed è compito dell'inferenza statistica esprimere
correttamente tale incertezza.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... misura.11.2
- `Fatto' è fra virgolette perché
non c'è nessuna necessità logica che ci obblighi ad adottare
tale modello; abbiamo soltanto ottimi argomenti, sia di natura
teorica che empirica che ci fanno pensare che molto probabilmente
sarà così.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... semplificazoni11.3
- A parte
fattori moltiplicativi, abbiamo
In particolare, nell'ultimo passaggio abbiamo ``complementato''
l'esponenziale moltiplicando e dividendo per
![$ \exp[-2\,\mu_A^2/\sigma_A^2]$](img3215.png) . Normalizzando, otteniamo la
11.7.
. Normalizzando, otteniamo la
11.7.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
nome11.4
- Vedi ad esempio F. Sibirani,
``Calcolo delle probabilità'',
in Enciclopedia delle Matematiche Elementari
e Complementari, a cura di L. Berzolati, Hoepli, 1949
(ristampa anastatica 1987), Volume III,
parte 2
 , pp. 234-236. Le citazioni in latino sono
dallo scritto originale di Gauss Theoria motus corporum coelestium
in sectionibus conicis solem ambientium'' del 1809.
Esse sono riportate per mostrare come l'impostazione di questo testo,
seppur moderna, se confrontata con la prassi statistica del XX secolo,
si rifà al modo di pensare originario sulla probabilità di Gauss,
Laplace, Bernoulli etc.
, pp. 234-236. Le citazioni in latino sono
dallo scritto originale di Gauss Theoria motus corporum coelestium
in sectionibus conicis solem ambientium'' del 1809.
Esse sono riportate per mostrare come l'impostazione di questo testo,
seppur moderna, se confrontata con la prassi statistica del XX secolo,
si rifà al modo di pensare originario sulla probabilità di Gauss,
Laplace, Bernoulli etc.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
vincolo11.5
- Il modo più semplice di usare la condizione di vincolo
quello di passare ai differenziali di
 :
:
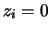 d
d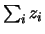 (
( ), con la condizione
), con la condizione
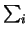 che si riflette in un'analoga condizione sui differenziali:
che si riflette in un'analoga condizione sui differenziali:
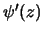 d
d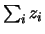 . Affinché (
. Affinché ( ) sia sempre valida,
) sia sempre valida,
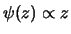 deve essere costante, da cui segue
deve essere costante, da cui segue
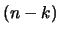 e quindi la (11.20).
e quindi la (11.20).
Un modo più vicino alla dimostrazione originale di Gauss
è di pensare al caso in cui  degli
degli  scarti acquistino il
valore
scarti acquistino il
valore  e gli altri
e gli altri 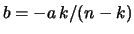 acquistino il valore
acquistino il valore 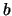 , con
, con
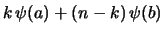 , in virtù degli vincolo della media aritmetica.
Abbiamo allora
, in virtù degli vincolo della media aritmetica.
Abbiamo allora
da cui
Poichè questa relazione non deve dipendere dal valore di  scelto,
e nemmeno da
scelto,
e nemmeno da  (nella dimostrazione originale di Gauss viene
preso in considerazione soltanto il caso
(nella dimostrazione originale di Gauss viene
preso in considerazione soltanto il caso 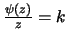 ), la condizione
), la condizione
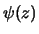 è assunta universale, e questa porta alla gaussiana.
è assunta universale, e questa porta alla gaussiana.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
ottenendo11.6
- Ad esempio, utilizzando il seguente integrale:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... abbiamo:11.7
- L'integrale
di interesse è
![$\displaystyle \int_0^\infty \! z^{-n}
\exp{\left[-\frac{C}{2\,z^2}\right]}
\,$](img3387.png)
d
![$\displaystyle z =
2^{(n-3)/2}\,\Gamma\left[\frac{1}{2}(n-1)\right]
C^{-(n-1)/2}.
$](img3388.png)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... precedente.11.8
- Non è raro
sentire o leggere che tale probabilità è del 68%. È chiaro
l'errore concettuale che si sta commettendo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sovrappongono11.9
- Questa affermazione vale per le regioni in cui
si ammassa il più alto grado di fiducia: avendo assunto un modello
gaussiano, in cui le variabili possono assumere valori su tutto
l'asse reale, le regioni di certezza (da
 a
a  ) si
sovrappongono sempre!
) si
sovrappongono sempre!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... prior11.10
- Soltanto il ``perfetto idiota'' (a trovarlo)
è esente da prior. Ma non è la persona giusta a cui
rivolgersi per aumentare la nostra conoscenza.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
generale11.11
- Si veda ad esempio G. D'Agostini, ``sceptiical ..''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
sono:12.1
- Si riconosce nella (12.11)
una distribuzione Beta
di parametri
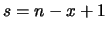 e
e 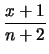 (vedi paragrafo 8.15.1).
Questa identificazione sarà usata nel seguito per introdurre
la distribuzione Beta come coniugata della binomiale in problemi
inferenziali.
(vedi paragrafo 8.15.1).
Questa identificazione sarà usata nel seguito per introdurre
la distribuzione Beta come coniugata della binomiale in problemi
inferenziali.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... condition14.1
- The case
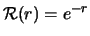 yields
yields
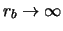 , obtainable starting directly
from Eq. (14.9), defining
, obtainable starting directly
from Eq. (14.9), defining 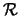 , and from
Eq. (14.1), giving the likelihood. Also the case
, and from
Eq. (14.1), giving the likelihood. Also the case
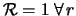 has to be evaluated directly from
the definition of
has to be evaluated directly from
the definition of 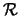 and from the likelihood,
yielding
and from the likelihood,
yielding
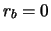 ; finally,
the case
; finally,
the case 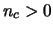 and
and  makes
makes 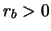 impossible, thus prompting
a claim for discovery -
and it no longer makes sense for the
impossible, thus prompting
a claim for discovery -
and it no longer makes sense for the 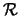 function
defined above to have that nice
asymptotic behaviour in the insensitivity region.
function
defined above to have that nice
asymptotic behaviour in the insensitivity region.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... must14.2
- It really is a `must' and not
a `suggestion'. In fact, although probabilities may depend
on individuals (`subjective'), the way they are updated
follows from standard logic (yielding Bayes' theorem) and thus
is `objective'.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... needed.14.3
- Note that, although
it is important to present prior-free results, at a
certain moment a probability assessment about
 can be important,
for example, in forming one's own idea about the most likely range
of
can be important,
for example, in forming one's own idea about the most likely range
of  , or in taking decisions
about planning and financing of future experiments.
, or in taking decisions
about planning and financing of future experiments.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... same14.4
- See comments about
the choice of the energy threshold in Section
![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
riduce15.1
- Se si prova a fare i conti
con le regole delle matematica elementare si trovano risultati
divergenti. In realtà il limite va fatto integrando la
funzione per tutti i valori di
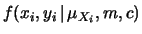 e quindi fare il limite per
e quindi fare il limite per
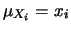 . Chi è familiare con elementi di matematica
avanzata riconosce in tale operazione l'uso della
. Chi è familiare con elementi di matematica
avanzata riconosce in tale operazione l'uso della 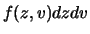 di Dirac
(vedi anche prossimo paragrafo).
di Dirac
(vedi anche prossimo paragrafo).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
rispettivamente16.1
- Le piccolissime differenze rispetto
alle previsioni intuitive di 2.3 e 2.1 V sono dovute alla
rozza schematizzazione dell'incertezza,
curabili modellizzando meglio il meccanismo di
arrotondamento o passando alle variabili
continue.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
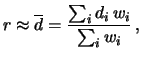 , ad esempio,
non è valutata dalla frequenza di zero morti nel passato.
Quindi, anche se si stanno utilizzando informazioni statistiche
la probabilità non è valutata secondo il paradigma frequentista.
, ad esempio,
non è valutata dalla frequenza di zero morti nel passato.
Quindi, anche se si stanno utilizzando informazioni statistiche
la probabilità non è valutata secondo il paradigma frequentista.
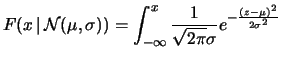
 d
d
 erf
erf
 , e così via.
Eviteremo questo modo più preciso (e pesante)
in quanto non ci sono ragioni per temere ambiguità. Allo stesso
modo gli estremi degli integrali saranno omessi a sottintendere
che essi si estendono su tutti i possibili valori di
, e così via.
Eviteremo questo modo più preciso (e pesante)
in quanto non ci sono ragioni per temere ambiguità. Allo stesso
modo gli estremi degli integrali saranno omessi a sottintendere
che essi si estendono su tutti i possibili valori di  d
d .
.
 è la delta di Kronecker che vale 1 se
è la delta di Kronecker che vale 1 se ![$\displaystyle \int_{-\infty}^{+\infty}\exp\left[bx-\frac{x^2}{a^2}\right]\,$](img2737.png) d
d![$\displaystyle x
= \sqrt{a^2\pi}\exp\left[\frac{a^2b^2}{4}\right]\,.$](img2738.png)
 ).
).
 con
con  non sono invece correlate in quanto, per dirlo in
modo semplice, appartengono a diversi esperimenti. Ad esempio,
la conoscenza del valore di
non sono invece correlate in quanto, per dirlo in
modo semplice, appartengono a diversi esperimenti. Ad esempio,
la conoscenza del valore di 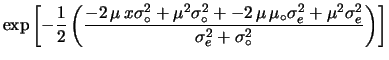
![$\displaystyle \exp\left[-\frac{1}{2}\left(
\frac{-2\,\mu\,x\sigma_\circ^2+\mu^2...
...mu_\circ\sigma_e^2+\mu^2\sigma_e^2
}
{\sigma_e^2+\sigma_\circ^2}
\right)\right]$](img3211.png)
![$\displaystyle \exp\left[-\frac{1}{2}\left(
\frac{\mu^2-2\,\mu\left(\frac{x\,\si...
...}
{(\sigma_e^2\cdot \sigma_\circ^2)/(\sigma_e^2+\sigma_\circ^2)}
\right)\right]$](img3212.png)
![$\displaystyle \exp\left[-\frac{1}{2}\left( \frac{\mu^2-2\mu \,\mu_A}{\sigma_A^2}
\right)\right]$](img3213.png)
![$ \exp[-2\,\mu_A^2/\sigma_A^2]$](img3215.png) . Normalizzando, otteniamo la
11.7.
. Normalizzando, otteniamo la
11.7.
![]() degli
degli ![]() scarti acquistino il
valore
scarti acquistino il
valore ![]() e gli altri
e gli altri ![]() acquistino il valore
acquistino il valore ![]() , con
, con
![]() , in virtù degli vincolo della media aritmetica.
Abbiamo allora
, in virtù degli vincolo della media aritmetica.
Abbiamo allora
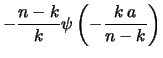
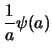
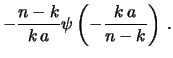
![$\displaystyle \int_{-\infty}^{+\infty}\!\exp{
\left[b\,x-\frac{x^2}{a^2}\right]}\,\mbox{d}x
= \sqrt{a^2\,\pi}\,\exp{\left[\frac{a^2\,b^2}{4}\right]}\,.$](img3324.png)
![$\displaystyle \int_0^\infty \! z^{-n}
\exp{\left[-\frac{C}{2\,z^2}\right]}
\,$](img3387.png) d
d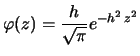 a
a