



Next: Gamma
Up: Altre distribuzioni di interesse
Previous: Altre distribuzioni di interesse
Indice
Beta
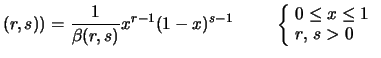 Beta Beta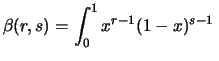 |
(8.36) |
Il denominarore ha il ruolo di costante di normalizzazione, ovvero
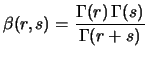
d
Questa funzione speciale, denominata ``beta'' e che dà il
nome alla distribuzione è calcolabile
dalle Gamma di Eulero mediante la relazione
ove, ricordiamo,
che per argomento  intero vale
intero vale
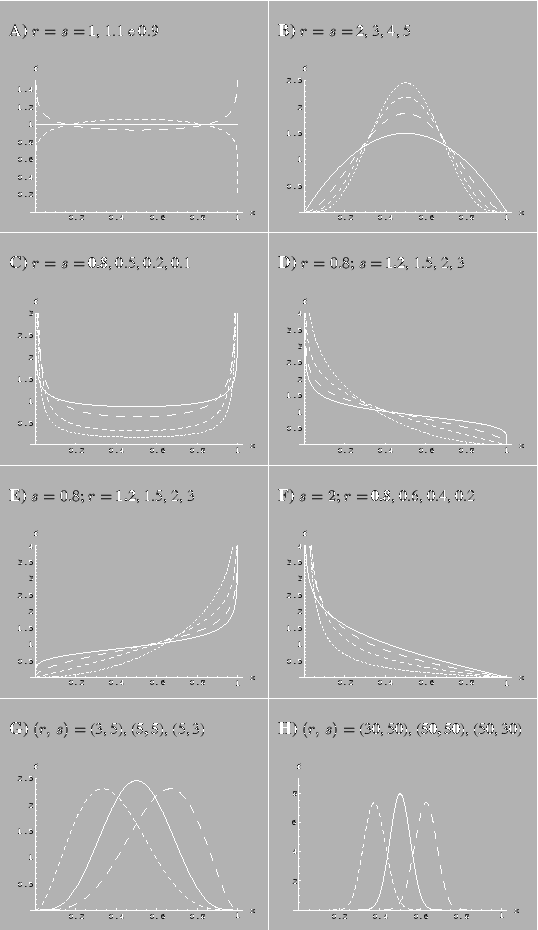
Figura:
Esempi di distribuzioni Beta per vari valori di  e
e 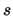 .
I numeri in grassetto si riferiscono alle curve continue.
.
I numeri in grassetto si riferiscono alle curve continue.
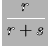 |
Valore atteso e varianza sono:
Se 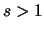 e
e 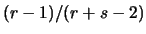 la moda è unica e vale
la moda è unica e vale
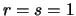 .
La figura 8.14 mostra come la distribuzione
beta possa assumere una ricca varietà di forme e quindi si presta
a modellizzare bene un certo numero di problemi. In particolare,
per
.
La figura 8.14 mostra come la distribuzione
beta possa assumere una ricca varietà di forme e quindi si presta
a modellizzare bene un certo numero di problemi. In particolare,
per 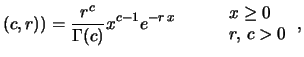 la distribuzione si riduce ad una distribuzione uniforme.
Si noti la somiglianza formale della (8.36), a meno
del fattore di normalizzazione, con l'espressione della distribuzione
binomiale, a meno del coefficiente binomiale. Vedremo infatti come
utilizzare tale proprietà formale per semplificare un classico
problema infernziale (vedi paragrafo 12.3).
la distribuzione si riduce ad una distribuzione uniforme.
Si noti la somiglianza formale della (8.36), a meno
del fattore di normalizzazione, con l'espressione della distribuzione
binomiale, a meno del coefficiente binomiale. Vedremo infatti come
utilizzare tale proprietà formale per semplificare un classico
problema infernziale (vedi paragrafo 12.3).




Next: Gamma
Up: Altre distribuzioni di interesse
Previous: Altre distribuzioni di interesse
Indice
Giulio D'Agostini
2001-04-02
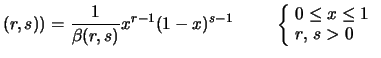 Beta
Beta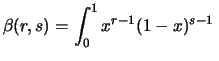
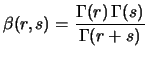 d
d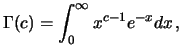
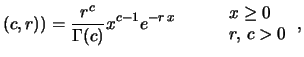 la distribuzione si riduce ad una distribuzione uniforme.
Si noti la somiglianza formale della (8.36), a meno
del fattore di normalizzazione, con l'espressione della distribuzione
binomiale, a meno del coefficiente binomiale. Vedremo infatti come
utilizzare tale proprietà formale per semplificare un classico
problema infernziale (vedi paragrafo 12.3).
la distribuzione si riduce ad una distribuzione uniforme.
Si noti la somiglianza formale della (8.36), a meno
del fattore di normalizzazione, con l'espressione della distribuzione
binomiale, a meno del coefficiente binomiale. Vedremo infatti come
utilizzare tale proprietà formale per semplificare un classico
problema infernziale (vedi paragrafo 12.3).