



Next: Distribuzione normale standardizzata
Up: Distribuzioni di probabilità di
Previous: pzd100Distribuzione esponenziale doppia
Indice
Distribuzione normale
Una distribuzione, in principio simile alla esponenziale
doppia per quanto riguarda la simmetria rispetto al valore centrale
e l'estensione a grandissimi scarti, ma che meglio si presta a
descrivere moltissimi casi di interesse
è quella in cui i gradi di fiducia vanno come
ove 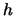 è una costante positiva. Questa funzione, opportunamente
normalizzata, è nota come
funzione di Gauss, o gaussiana.
Essa deve il nome a Karl Friederick Gauss, che la propose
per la descrizione delle deviazioni delle misure astronomiche
rispetto al loro andamento medio.
Egli ipotizzò infatti che tali deviazioni fossero dovute
ad errori casuali di misura e, in base ad argomenti
abbastanza generali, derivò una
funzione densità di probabilità
del tipo appena mostrato
(vedi paragrafo 11.4.
Stanti i forti argomenti teorici per ritenere che gli errori casuali
debbano seguire tale distribuzione (vedi paragrafo
10.15 e 11.2)
e la effettiva compatibilità
dei dati sperimentali con tale ipotesi, viene comunemente detto che
gli errori casuali ``seguono normalmente'' tale distribuzione
e la distribuzione stessa è perciò chiamata
anche distribuzione normale.
è una costante positiva. Questa funzione, opportunamente
normalizzata, è nota come
funzione di Gauss, o gaussiana.
Essa deve il nome a Karl Friederick Gauss, che la propose
per la descrizione delle deviazioni delle misure astronomiche
rispetto al loro andamento medio.
Egli ipotizzò infatti che tali deviazioni fossero dovute
ad errori casuali di misura e, in base ad argomenti
abbastanza generali, derivò una
funzione densità di probabilità
del tipo appena mostrato
(vedi paragrafo 11.4.
Stanti i forti argomenti teorici per ritenere che gli errori casuali
debbano seguire tale distribuzione (vedi paragrafo
10.15 e 11.2)
e la effettiva compatibilità
dei dati sperimentali con tale ipotesi, viene comunemente detto che
gli errori casuali ``seguono normalmente'' tale distribuzione
e la distribuzione stessa è perciò chiamata
anche distribuzione normale.
Imponendo la condizione di normalizzazione
e ridefinendo
opportunamente i parametri
in modo tale da far apparire esplicitamente valore atteso
e deviazione standard
della distribuzione otteniamo la forma nella quale essa è
comunemente conosciuta:
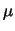 |
(8.15) |
Quindi (anche se non lo dimostriamo):
Questa distribuzione ricopre un ruolo notevole
non soltanto per la descrizione degli errori casuali, ma anche
perchè essa risulta essere la distribuzione a cui tendono, sotto
condizioni generali che descriveremo, molte altre distribuzioni,
comprese la binomiale e la poissoniana.
Elenchiamo le sue proprietà principali:
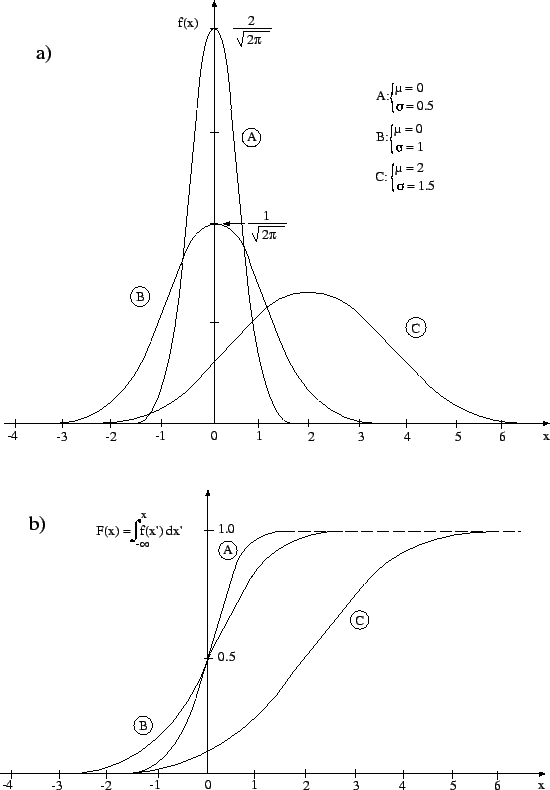
Figura:
Esempi di distribuzione normale.
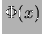 |
La figura 8.5a mostra
degli esempi di distribuzione normale, per alcuni valori di
 e di
e di  .
Nella figura 8.5b
è anche riportata, per ciascuna
.
Nella figura 8.5b
è anche riportata, per ciascuna 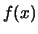 , la
relativa funzione di
ripartizione8.3
, la
relativa funzione di
ripartizione8.3
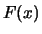 , la cui espressione
matematica è data, per definizione::
, la cui espressione
matematica è data, per definizione::
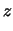 d d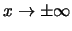 |
(8.16) |
Purtroppo l'integrale non ha una forma semplice. Vedremo
nel prossimo paragrafo come
valutarla mediante opportune tabelle. Anche senza
l'espressione analitica,
possiamo elencare alcune
proprietà della funzione di ripartizione, ottenibili
direttamente da quelle della 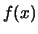 :
:
- ha una forma di ``
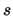 allungata'' (sigmoide) con asintoti
orizzontali per
allungata'' (sigmoide) con asintoti
orizzontali per
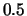 ;
;
- assume il valore
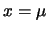 per
per 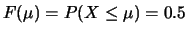 , in quanto
, in quanto
 ;
;
- ha un andamento
pressoché lineare intorno a
 , con pendenza inversamente
proporzionale a
, con pendenza inversamente
proporzionale a  ;
;
- ha un punto di flesso, ovvero cambia curvatura,
in corrispondenza di
 .
.
Figura:
Rappresentazione su scala delle ordinate logaritmica
della distribuzione normale standardizzata (
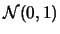 ).
).
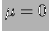 |
Per fare apprezzare meglio gli andamenti delle code della distribuzione
la figura 8.6 mostra
su su scala logaritmica la distribuzione normale
avente  e
e 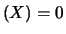 .
.
Figura:
Distribuzioni di Laplace, di Gauss, triangolare e uniforme
aventi
E e
e
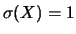 .
.
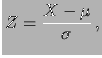 |




Next: Distribuzione normale standardizzata
Up: Distribuzioni di probabilità di
Previous: pzd100Distribuzione esponenziale doppia
Indice
Giulio D'Agostini
2001-04-02
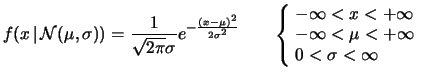
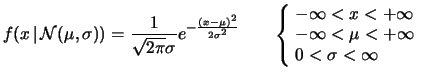
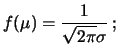 ) è inversamente
proporzionale alla deviazione
standard8.2:
) è inversamente
proporzionale alla deviazione
standard8.2:
 ;
;