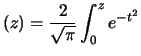Next: Uso delle tabelle dell'integrale
Up: Distribuzioni di probabilità di
Previous: Distribuzione normale
Indice
Essendo la distribuzione normale largamente utilizzata e non avendo
il suo integrale indefinito una forma analitica, per
il calcolo delle probabilità vengono usati valori tabulati.
Si capisce bene che sarebbe impossibile avere tabelle per
tutte le possibili coppie di valori dei parametri.
È quindi conveniente rendere il calcolo
della funzione di ripartizione
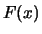 indipendente dai parametri.
Eseguendo la seguente trasformazione di variabili:
otteniamo quindi che la probabilità che la variabile sia compresa fra
indipendente dai parametri.
Eseguendo la seguente trasformazione di variabili:
otteniamo quindi che la probabilità che la variabile sia compresa fra
 e
e 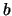 vale
vale
La variabile 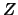 è chiamata variabile normale
standardizzata e la funzione di probabilità
è chiamata variabile normale
standardizzata e la funzione di probabilità
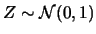 |
(8.17) |
è detta distribuzione normale standardizzata.
La variabile 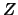 corrisponde ad una ``trasformazione di coordinate
lungo l'asse X tale da misurare la variabile in unità di
corrisponde ad una ``trasformazione di coordinate
lungo l'asse X tale da misurare la variabile in unità di
 a partire dal
punto
a partire dal
punto 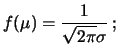 '' (vedi figura 8.9).
Come si vede facilmente, la distribuzione normale standardizzata
è una particolare normale di valor medio nullo e varianza unitaria:
'' (vedi figura 8.9).
Come si vede facilmente, la distribuzione normale standardizzata
è una particolare normale di valor medio nullo e varianza unitaria:
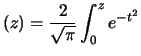 |
(8.18) |




Next: Uso delle tabelle dell'integrale
Up: Distribuzioni di probabilità di
Previous: Distribuzione normale
Indice
Giulio D'Agostini
2001-04-02
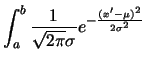
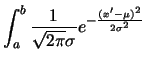
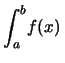
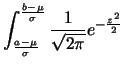
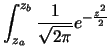 d
d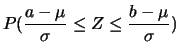
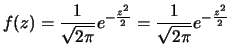
![]() è chiamata variabile normale
standardizzata e la funzione di probabilità
è chiamata variabile normale
standardizzata e la funzione di probabilità
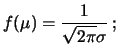 '' (vedi figura 8.9).
Come si vede facilmente, la distribuzione normale standardizzata
è una particolare normale di valor medio nullo e varianza unitaria:
'' (vedi figura 8.9).
Come si vede facilmente, la distribuzione normale standardizzata
è una particolare normale di valor medio nullo e varianza unitaria: