



Next: Binomiale
Up: Distribuzioni di probabilità di
Previous: Assenza di memoria di
Indice
pzd100 Funzione generatrice
dei momenti
Questo paragrafo, decisamente tecnico, mostra come sia possibile
calcolare in modo relativamente semplice i momenti delle
distribuzioni (e da questi, ad esempio,
media e deviazione standard),
facendo uso di proprietà formali dei valori attesi.
Consideriamo il valore atteso della funzione 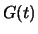 ,
dove
,
dove  rappresenta un parametro che può assumere con
continuità valori reali, ed indichiamolo con
rappresenta un parametro che può assumere con
continuità valori reali, ed indichiamolo con 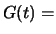 :
:
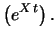 E E |
(8.30) |
L'interesse di questo valore atteso risiede nella proprietà matematica
di cui esso gode. Espandendo 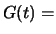 in serie di Taylor intorno a
in serie di Taylor intorno a
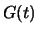 si ha infatti:
si ha infatti:
Otteniamo che i coefficienti dell'espansione sono proporzionali ai momenti
intorno a zero, essendo
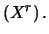
E
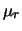
(si noti che  è un parametro e non un numero aleatorio).
è un parametro e non un numero aleatorio).
Se effettuiamo la derivata di ordine  di
di 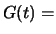 rispetto a
rispetto a  ,
il primo termine non nullo è
,
il primo termine non nullo è 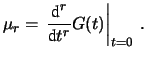 , mentre tutti i termini
successivi sono
proporzionali ai momenti di ordine superiore a
, mentre tutti i termini
successivi sono
proporzionali ai momenti di ordine superiore a  ,
moltiplicati per potenze di
,
moltiplicati per potenze di  .
Prendendo il valore della derivata
.
Prendendo il valore della derivata  -esima di
-esima di 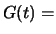 , calcolata
in
, calcolata
in 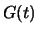 , possiamo allora isolare quindi il momento di ordine
, possiamo allora isolare quindi il momento di ordine  :
:
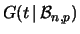 |
(8.31) |
A causa della notevole
proprietà di cui 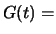 , essa
è nota come funzione generatrice dei momenti.
La sua utilità risiede nel fatto che a volte è più semplice
ricavarsi
, essa
è nota come funzione generatrice dei momenti.
La sua utilità risiede nel fatto che a volte è più semplice
ricavarsi
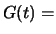 una volta per tutte e ottenere i momenti mediante derivate
che effettuare gli integrali o le sommatorie necessarie
per il loro calcolo diretto.
una volta per tutte e ottenere i momenti mediante derivate
che effettuare gli integrali o le sommatorie necessarie
per il loro calcolo diretto.
Applichiamo questa tecnica ad alcune
della distribuzioni incontrate, lasciando come
esercizio il caso della distribuzione esponenziale:
Subsections




Next: Binomiale
Up: Distribuzioni di probabilità di
Previous: Assenza di memoria di
Indice
Giulio D'Agostini
2001-04-02
![]() ,
dove
,
dove ![]() rappresenta un parametro che può assumere con
continuità valori reali, ed indichiamolo con
rappresenta un parametro che può assumere con
continuità valori reali, ed indichiamolo con ![]() :
:
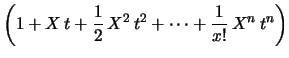
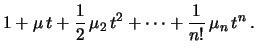
![]() di
di ![]() rispetto a
rispetto a ![]() ,
il primo termine non nullo è
,
il primo termine non nullo è 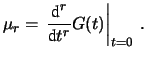 , mentre tutti i termini
successivi sono
proporzionali ai momenti di ordine superiore a
, mentre tutti i termini
successivi sono
proporzionali ai momenti di ordine superiore a ![]() ,
moltiplicati per potenze di
,
moltiplicati per potenze di ![]() .
Prendendo il valore della derivata
.
Prendendo il valore della derivata ![]() -esima di
-esima di ![]() , calcolata
in
, calcolata
in ![]() , possiamo allora isolare quindi il momento di ordine
, possiamo allora isolare quindi il momento di ordine ![]() :
: