



Next: Estensione del teorema del
Up: Teorema del limite centrale
Previous: Distribuzione della media aritmetica
Indice
Sia la binomiale che la poissoniana godono della proprietà riproduttiva.
Questa proprietà permette di pensare una distribuzione caratterizzata
da un valore medio elevato come una somma di tante variabili casuali
provenienti dallo stesso tipo di distribuzione
ma caratterizzate da valori medi più piccoli.
Siccome per il teorema del limite centrale una somma di
variabili casuali tende ad una distribuzione normale,
la distribuzione binomiale e quella di Poisson tendono alla
distribuzione normale al crescere, rispettivamente, di 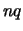 e di
e di
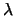 :
:
- distribuzione binomiale:
per valori di
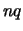 e di
e di 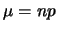 ``abbastanza grandi'' la distribuzione binomiale tende
ad una distribuzione normale di
``abbastanza grandi'' la distribuzione binomiale tende
ad una distribuzione normale di 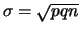 e
e
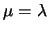 ;
;
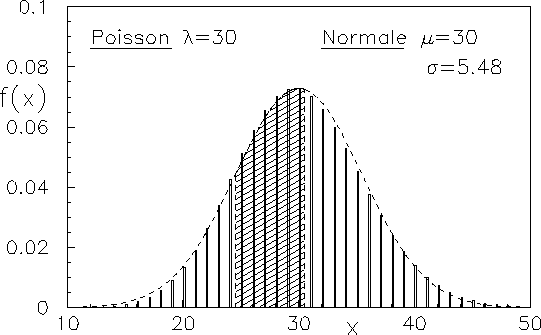
- distribuzione di Poisson:
per valori di
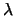 ``abbastanza grandi'' la distribuzione di Poisson tende
ad una distribuzione normale di
``abbastanza grandi'' la distribuzione di Poisson tende
ad una distribuzione normale di
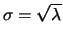 e
e
 .
.
La condizione di valore
``abbastanza grande'' dipende dal grado di accuratezza
con cui si vuole calcolare la probabilità. Per la maggior parte delle
applicazioni che si incontrano nella trattazione degli errori e per
la determinazione degli intervalli di fiducia la condizione è soddisfatta
per valori di 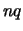 ,
, 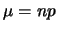 e
e 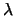 maggiori di 10-15.
maggiori di 10-15.
Figura:
Approssimazione normale della distribuzione di Poisson.
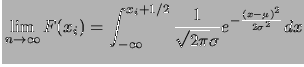 |
Bisogna precisare cosa si intende per
limite di una distribuzione discreta
a una distribuzione continua. Infatti in un caso la funzione di distribuzione
ha il significato di una probabilità e nell'altro di una densità di
probabilità. Il limite va allora inteso per la funzione di ripartizione:
dove l'integrale è stato esteso
fino a 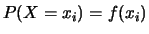 per tener conto della natura discreta della variabile
casuale. Otteniamo quindi per la probabilità di un determinato
valore della variabile casuale:
per tener conto della natura discreta della variabile
casuale. Otteniamo quindi per la probabilità di un determinato
valore della variabile casuale:
dove abbiamo utilizzato il fatto
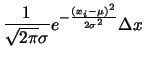 per le
distribuzioni discrete di interesse.
per le
distribuzioni discrete di interesse.
A volte, se si è interessati
alla probabilità di un solo valore 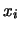 ,
l'integrale viene ignorato e la distribuzione normale
viene utilizzata come se fosse una distribuzione discreta.
Questo deriva dall'approssimazione
,
l'integrale viene ignorato e la distribuzione normale
viene utilizzata come se fosse una distribuzione discreta.
Questo deriva dall'approssimazione
essendo
 .
.
Figura:
Proprietà asintotiche della distribuzione binomiale
e di quella di Poisson.
 |




Next: Estensione del teorema del
Up: Teorema del limite centrale
Previous: Distribuzione della media aritmetica
Indice
Giulio D'Agostini
2001-04-02
 .
.
 .
.
![]() ,
, ![]() e
e ![]() maggiori di 10-15.
maggiori di 10-15.
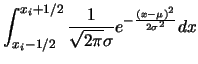
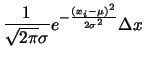 per le
distribuzioni discrete di interesse.
per le
distribuzioni discrete di interesse.
![]() ,
l'integrale viene ignorato e la distribuzione normale
viene utilizzata come se fosse una distribuzione discreta.
Questo deriva dall'approssimazione
,
l'integrale viene ignorato e la distribuzione normale
viene utilizzata come se fosse una distribuzione discreta.
Questo deriva dall'approssimazione
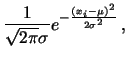
 .
.