Se si eseguono contemporaneamente
tante scommesse su tanti eventi ![]() ,
,
![]() ,...,
,..., ![]() , la speranza matematica è la somma delle speranza
matematiche di ciascuna delle scommesse. Includendo anche l'evento
, la speranza matematica è la somma delle speranza
matematiche di ciascuna delle scommesse. Includendo anche l'evento
![]() (``non si verifica nessuno degli altri
(``non si verifica nessuno degli altri ![]() eventi''),
con vincita nulla (
eventi''),
con vincita nulla (![]() ), otteniamo
), otteniamo
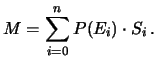 |
(2.16) |
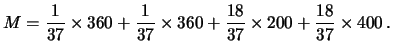
Questi termini potrebbero generare
confusione se non li si pensa accompagnati dall'aggettivo ``probabilistico'',
e si intendesse che vogliano dire ``predizioni'' in termini di certezza.
Non si deve nemmeno intendere che essi si riferiscano agli importi che
effettivamente si possono vincere (0, ![]() ,
, ![]() , etc).
L'esempio della roulette rende abbastanza bene l'idea. Le possibili
vincite sono 0 (non si realizza nessuna delle puntate), 200 mila
(un pari che non sia il ``2'' e nemmeno ``rosso''), 560 o 960 mila
se esce il ``2'' (nelle due ipotesi che questo numero sia definito nero
o rosso), e così via.
, etc).
L'esempio della roulette rende abbastanza bene l'idea. Le possibili
vincite sono 0 (non si realizza nessuna delle puntate), 200 mila
(un pari che non sia il ``2'' e nemmeno ``rosso''), 560 o 960 mila
se esce il ``2'' (nelle due ipotesi che questo numero sia definito nero
o rosso), e così via.
Quindi l'attesa, o previsione, probabilistica dà l'idea di una sorta di vincita media, e su questo concetto ritorneremo quando si parlerà delle variabili casuali. Quello che è importante è che, in scommesse eque, la previsione di vincita deve essere uguale alla somma delle poste.
Estendiamo il concetto di scommessa a situazioni più complicate
in cui si gioca contemporaneamente pro e contro diversi eventi. Ovvero
per alcuni eventi ![]() può essere positivo e per altri può essere
negativo. Questo è quello che si verifica tutti i giorni quando
possono accadere degli eventi in grado di produrre vantaggi o svantaggi
a seconda che si verifichino oppure no: affrontare un viaggio per
procurarsi un lavoro comporta una spesa che potrebbe essere compensata
dall'assunzione; viaggiare sull'autobus senza biglietto ha un vantaggio
immediato che però può trasformarsi in una perdita se passa il controllore.
Anche la roulette può essere vista in questo modo considerando la
puntata
può essere positivo e per altri può essere
negativo. Questo è quello che si verifica tutti i giorni quando
possono accadere degli eventi in grado di produrre vantaggi o svantaggi
a seconda che si verifichino oppure no: affrontare un viaggio per
procurarsi un lavoro comporta una spesa che potrebbe essere compensata
dall'assunzione; viaggiare sull'autobus senza biglietto ha un vantaggio
immediato che però può trasformarsi in una perdita se passa il controllore.
Anche la roulette può essere vista in questo modo considerando la
puntata ![]() una perdita quando non si verifica nessuno degli eventi
sui quali si è scommesso.
una perdita quando non si verifica nessuno degli eventi
sui quali si è scommesso.
In questi casi, al posto della previsione di vincita (calcolata senza
tener conto della posta pagata) è preferibile parlare della previsione
di guadagno, ottenuta con la stessa formula di ![]() e indicata con
I
e indicata con
I![]() P
P![]() e calcolata in due modi
alternativi ma equivalenti:
e calcolata in due modi
alternativi ma equivalenti:
I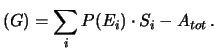 |
(2.18) |
| I |
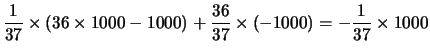 |
||
| I |
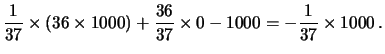 |
Come esempio di decisione,
consideriamo la situazione di un automobilista che deve scegliere
fra pagare il biglietto
del parchimetro, di costo ![]() , o
rischiare una multa di importo
, o
rischiare una multa di importo ![]() se arriva il
vigile, evento la cui probabilità
se arriva il
vigile, evento la cui probabilità
![]() è subordinata allo stato
di informazione su
città, quartiere, ora, traffico, situazione meteorologica,
etc. La previsione di guadagno è
è subordinata allo stato
di informazione su
città, quartiere, ora, traffico, situazione meteorologica,
etc. La previsione di guadagno è
| I |
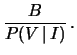 |