come detto, rappresenta qualsiasi affermazione. Nel
caso dei dadi possiamo avere ad esempio: ``2'', ``pari'',
``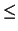 3'', ``1, 2, 5'', etc. Questi eventi vengono indicati generalmente
con lettere maiuscole:
3'', ``1, 2, 5'', etc. Questi eventi vengono indicati generalmente
con lettere maiuscole:  ,
,  ,
,  , etc. A volte si usa
, etc. A volte si usa 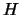 , a
indicare
``ipotesi'', in quanto gli eventi sono associati ad ipotesi (``nell'ipotesi
che esce il sei vinco'').
, a
indicare
``ipotesi'', in quanto gli eventi sono associati ad ipotesi (``nell'ipotesi
che esce il sei vinco'').
A volte si indicano con lettere minuscole
gli eventi elementari, volendo con essi indicare
descrizioni di avvenimenti che non possono essere
classificati ulteriormente in base a caratteristiche che hanno alcuni
e non altri.
Quindi nel caso del dado si avrebbe: 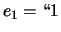 '',
'', 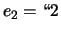 ''.
''.
(Si noti che nei casi reali
non ha senso parlare di eventi elementari,
in quanto, dato un certo avvenimento,
le caratterizzazioni possono essere
virtualmente infinite. Ad esempio l'evento ``la squadra  vince''
può essere caratterizzata da ``se gioca in casa'', ``con almeno due
goal di scarto'', ``nonostante il portiere espulso'', etc.)
vince''
può essere caratterizzata da ``se gioca in casa'', ``con almeno due
goal di scarto'', ``nonostante il portiere espulso'', etc.)
Un modo generale di indicare gli eventi del lancio del dado è
di elencare i casi elementari che li costituiscono, come ad esempio
- -
 = ``pari'' = {2, 4, 6};
= ``pari'' = {2, 4, 6};
- -
 = ``
= ``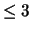 '' = {1, 2, 3};
'' = {1, 2, 3};
- -
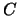 = ``6'' =
= ``6'' = 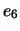 = {6}.
= {6}.
![]() '',
'', ![]() ''.
''.
![]() vince''
può essere caratterizzata da ``se gioca in casa'', ``con almeno due
goal di scarto'', ``nonostante il portiere espulso'', etc.)
vince''
può essere caratterizzata da ``se gioca in casa'', ``con almeno due
goal di scarto'', ``nonostante il portiere espulso'', etc.)

