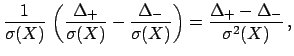Next: Uncertainty due to systematics
Up: Sources of asymmetric uncertainties
Previous: Non parabolic or log-likelihood
Nonlinear propagation
Another source of asymmetric uncertainties is
nonlinear dependence of the output quantity 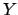 on some of the input
on some of the input
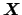 in a
region a few standard deviations
around
in a
region a few standard deviations
around
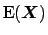 .
This problem has been studied with great detail
in Ref. [2],
also taking into account correlations
on input and output quantities,
and somewhat summarized in
Ref. [3].
Let us recall here only the most relevant outcomes,
in the simplest case of only one output quantity
.
This problem has been studied with great detail
in Ref. [2],
also taking into account correlations
on input and output quantities,
and somewhat summarized in
Ref. [3].
Let us recall here only the most relevant outcomes,
in the simplest case of only one output quantity 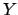 and neglecting correlations.
and neglecting correlations.
Figure:
Propagation of a
Gaussian distribution under a nonlinear transformation.
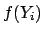 were obtained analytically using
Eq.(1) (part of Fig. 12.2 of Ref.[3]).
were obtained analytically using
Eq.(1) (part of Fig. 12.2 of Ref.[3]).
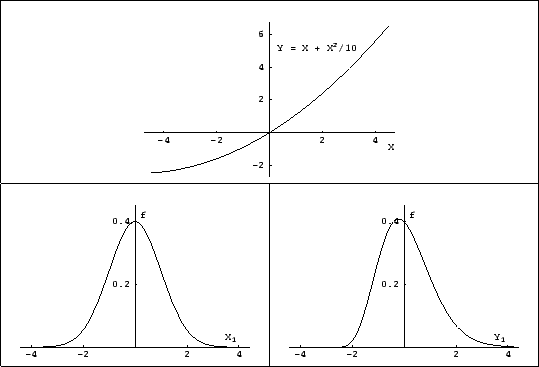 |
Figure 4 shows a non linear dependence between
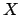 and
and 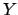 and how a Gaussian distribution has been distorted
by the transformation [
and how a Gaussian distribution has been distorted
by the transformation [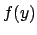 has been
evaluated analytically using Eq.(1)].
As a result of the nonlinear transformation,
mode, mean, median and standard deviation
are transformed in non trivial ways (in the example of
Fig. 4 mode moves left and expected value right).
In the general case
the complete calculations should be performed,
either analytically, or numerically or by Monte Carlo.
Fortunately,
as it has been shown in Ref. [2], second order
expansion is often enough to take into account small
deviations from linearity. The resulting formulae
are still compact and depend on location and shape
parameters of the
initial distributions.
has been
evaluated analytically using Eq.(1)].
As a result of the nonlinear transformation,
mode, mean, median and standard deviation
are transformed in non trivial ways (in the example of
Fig. 4 mode moves left and expected value right).
In the general case
the complete calculations should be performed,
either analytically, or numerically or by Monte Carlo.
Fortunately,
as it has been shown in Ref. [2], second order
expansion is often enough to take into account small
deviations from linearity. The resulting formulae
are still compact and depend on location and shape
parameters of the
initial distributions.
Second order propagation formulae depend on first
and second derivatives.
In practical cases (especially
as far as the contribution from systematic effects are concerned)
the derivatives are obtained
numerically9 as
where 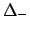 and
and 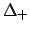 now stand for the left and right deviations of
now stand for the left and right deviations of 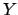 when the input variable
when the input variable 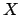 varies by one standard deviation
around
varies by one standard deviation
around ![$\mbox{E}[X]$](img121.png) .
Second order propagation formulae
are conveniently given
in Ref. [2] in terms of the
.
Second order propagation formulae
are conveniently given
in Ref. [2] in terms of the  deviations10.
For
deviations10.
For 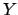 that depends only on a single
input
that depends only on a single
input 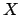 we get:
we get:
where 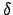 is the semi-difference of the two deviations
and
is the semi-difference of the two deviations
and
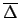 is their average:
is their average:
while 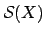 and
and 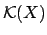 stand for skewness and kurtosis
of the input variable.11
stand for skewness and kurtosis
of the input variable.11
For many input quantities we have
where
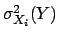 stands for each individual contribution to
Eq. (22). The expression of the variance
gets simplified
when all input quantities are Gaussian
(a Gaussian has skewness equal 0
and kurtosis equal 3):
stands for each individual contribution to
Eq. (22). The expression of the variance
gets simplified
when all input quantities are Gaussian
(a Gaussian has skewness equal 0
and kurtosis equal 3):
and, as long as 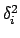 are much smaller that
are much smaller that
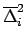 , we get the convenient
approximated formulae
, we get the convenient
approximated formulae
valid also for other symmetric input p.d.f.'s (the kurtosis is
about 2 to 3 in typical distribution and its exact value
is irrelevant
if the condition
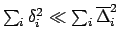 holds).
The resulting practical rules
(28)-(29)
are quite simple:
holds).
The resulting practical rules
(28)-(29)
are quite simple:
- the expected value of
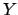 is shifted
by the sum of the individual shifts,
each given by half of the semi-difference of the deviations
is shifted
by the sum of the individual shifts,
each given by half of the semi-difference of the deviations  ;
;
- each input quantity contributes (in quadrature) to the
combined standard uncertainty
with a term which is approximately the average between the
deviations
 .
.
Moreover, if there are many contributions to the uncertainty,
the final uncertainty
will be symmetric and approximately Gaussian,
thanks to the central limit theorem.



Next: Uncertainty due to systematics
Up: Sources of asymmetric uncertainties
Previous: Non parabolic or log-likelihood
Giulio D'Agostini
2004-04-27


![$\displaystyle \left.\frac{\partial Y}{\partial X}\right\vert _{\mbox{\small E}[X]}$](img117.png)
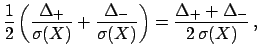
![$\displaystyle \left.\frac{\partial^2 Y}{\partial X^2}\right\vert _{\mbox{\small E}[X]}$](img119.png)