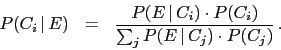Let us come finally to proposition (3): rational people are
ready to change their opinion in front of `enough'
experimental evidence. What is enough?
It is quite well understood that it all depends on
- how the new thing differs from from our initial beliefs;
- how strong our initial beliefs are.
This is the reason why practically nobody took very
seriously the CDF claim (not even most
members of the collaboration, and I know several of them),
while practically everybody is now convinced that the Higgs
boson has been finally caught at
CERN[31] - no matter if the
so called `statistical significance' is more ore less
the same in both cases (which was, by the way, more
or less the same for the excitement at CERN described
in footnote11 - nevertheless, the degree
of belief of a Higgs boson found at CERN is substantially different!).
Probability theory teaches us how to update the degrees of
belief on the different causes that might
be responsible of an `event' (read `experimental data'),
as simply explained by Laplace in his
Philosophical essay[17]
(`VI principle'14
at pag. 17 of the original book,
available at book.google.com - boldface is mine):
``The greater the probability of an observed event given any one
of a number of causes to which that event may be attributed,
the greater the likelihood15 of that cause {given that event}.
The probability of the existence of any one of these causes
{given the event} is thus a fraction
whose numerator is the probability of the event given the cause,
and whose denominator is the sum of similar probabilities,
summed over all causes. If the various causes are not equally probable
a priory, it is necessary, instead of the probability of the event
given each cause, to use the product of this probability
and the possibility
of the cause itself. This is the fundamental principle
of that branch of the analysis of chance
that consists of reasoning a posteriori from events
to causes.''
This is the famous Bayes' theorem (although Bayes
did not really derive this formula, but only
developed a similar inferential
reasoning for the parameter of Bernoulli
trials16) that we rewrite
in mathematical terms [omitting the subjective
`background condition' 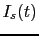 that should appear - and be the same! -
in all probabilities of the same equation] as
that should appear - and be the same! -
in all probabilities of the same equation] as
This formula teaches us that what matters is not (only)
how much
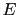 is probable in the light of
is probable in the light of 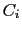 (unless it is impossible, in which case
(unless it is impossible, in which case
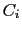 it is ruled out -
it is falsified to use a Popperian expression), but rather
it is ruled out -
it is falsified to use a Popperian expression), but rather
- how much
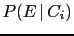 compares with
compares with 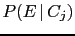 , where
, where
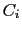 and
and 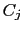 are two distinguished causes that could be
responsible of the same effect;
are two distinguished causes that could be
responsible of the same effect;
- how much
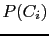 compares to
compares to 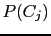 .
.
The essence of the Laplace(-Bayes) rule can
be emphasized writing the above formula for any couple of causes
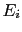 and
and 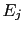 as
as
the odds are updated by the observed effect 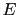 by a factor (`Bayes factor') given by the
ratio of the probabilities of the two causes to produce that
effect.
by a factor (`Bayes factor') given by the
ratio of the probabilities of the two causes to produce that
effect.
In particular, we learn that:
- It makes no sense to speak about how the probability
of
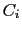 changes if:
changes if:
- there is no alternative cause
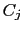 ;
;
- the way how
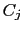 might produce
might produce 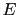 has not been modelled,
i.e. if
has not been modelled,
i.e. if 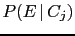 has not been somehow assessed.
has not been somehow assessed.
- The updating depends only on the Bayes factor,
a function of the probability of
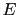 given either
hypotheses, and not on the probability of other
events that have not been observed and
that are even less probable than
given either
hypotheses, and not on the probability of other
events that have not been observed and
that are even less probable than 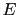 (upon which
p-values are instead calculated).
(upon which
p-values are instead calculated).
- One should be careful not to confuse
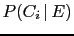 with
with 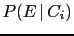 , and in general,
, and in general, 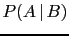 with
with 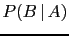 . Or, moving to continuous variables,
. Or, moving to continuous variables,
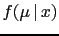 with
with 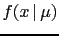 , where `
, where `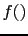 ' stands,
depending on the contest,
for a probability function
or for a probability density function,
while
' stands,
depending on the contest,
for a probability function
or for a probability density function,
while 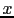 and
and 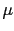 stand for an observed quantity and
a true value, respectively.
stand for an observed quantity and
a true value, respectively.
In particular the latter points looks rather trivial,
as it can be seen from the 'senator Vs woman' example of the
abstract. But already the Gaussian generator example there
might confuse somebody, while the `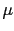 Vs
Vs 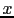 '
example is a typical source of misunderstandings, also because
in the statistical jargon
'
example is a typical source of misunderstandings, also because
in the statistical jargon 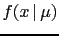 is called
`likelihood' function of
is called
`likelihood' function of 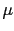 , and many practitioners
think it describes the probabilistic assessment concerning
the possible values of
, and many practitioners
think it describes the probabilistic assessment concerning
the possible values of 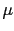 (again misuse of words! - for further comments see Appendix H
of [5]).
(again misuse of words! - for further comments see Appendix H
of [5]).
Giulio D'Agostini
2012-01-02