



Next: Are the beliefs in
Up: Appendix on probability and
Previous: Frequentists and combinatorial evaluation
Contents
Interpretation of conditional probability
As repeated throughout these notes, and
illustrated with many examples,
probability is always conditioned probability. Absolute
probability makes no sense. Nevertheless, there is still something
in the primer which can be misleading and that needs to
be clarified, namely the so-called `formula of conditional probability'
(Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ):
):
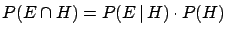 |
(8.1) |
What does it mean? Textbooks present it as
a definition (a kind of 4th axiom), although very often,
a few lines later in the same book,
the formula
 is presented as a theorem (!).
is presented as a theorem (!).
In the subjective approach, one is allowed to talk about
 independently of
independently of
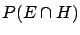 and
and 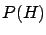 .
In fact,
.
In fact,
 is just the assessment of the probability
of
is just the assessment of the probability
of  , under the condition that
, under the condition that  is true. Then it cannot
depend on the probability of
is true. Then it cannot
depend on the probability of  . It is easy to show with an example
that this point of view is rather natural, whilst that of considering
(
. It is easy to show with an example
that this point of view is rather natural, whilst that of considering
(![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) as a definition is artificial. Let us take
) as a definition is artificial. Let us take
 = Higgs mass of 250 GeV;
= Higgs mass of 250 GeV;
 = the decay products which are detected in a LHC detector;
= the decay products which are detected in a LHC detector;
- the evaluation of
 is a standard PhD student task.
He chooses
is a standard PhD student task.
He chooses
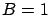 GeV
in the Monte Carlo and
counts how many events pass the cuts
(for the interpretation
of this operation, see the previous section). No one would
think that
GeV
in the Monte Carlo and
counts how many events pass the cuts
(for the interpretation
of this operation, see the previous section). No one would
think that
 must be evaluated only
from
must be evaluated only
from
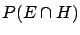 and
and 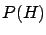 ,
as the definition (
,
as the definition (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) would imply.
Moreover, the procedure is legitimate even if we knew with
certainty that the Higgs mass was below 200 GeV and, therefore,
) would imply.
Moreover, the procedure is legitimate even if we knew with
certainty that the Higgs mass was below 200 GeV and, therefore,
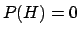 .
.
In the subjective approach,
(![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) is a true theorem required by coherence.
It means that although one can speak of each of the three
probabilities independently of the others, once two of them have been
elicited, the third is constrained. It is interesting
to demonstrate the theorem to show that it has nothing to do with
the kind of heuristic derivation of Section
) is a true theorem required by coherence.
It means that although one can speak of each of the three
probabilities independently of the others, once two of them have been
elicited, the third is constrained. It is interesting
to demonstrate the theorem to show that it has nothing to do with
the kind of heuristic derivation of Section
![[*]](file:/usr/lib/latex2html/icons/crossref.png) :
:
- Let us imagine a coherent bet
on the conditional event
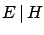 to win a unitary
amount of money (
to win a unitary
amount of money (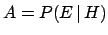 , as the scale factor is inessential).
Remembering the meaning of conditional probability in terms of bets (see
Section
, as the scale factor is inessential).
Remembering the meaning of conditional probability in terms of bets (see
Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ),
this means that
),
this means that
- we pay (with certainty)
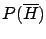 ;
;
- we win 1 if
 and
and  are both verified (with probability
are both verified (with probability
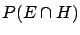 );
);
- we get our money back (i.e.
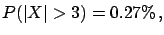 ) if
) if  does not happen
(with probability
does not happen
(with probability
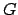 ).
).
- The expected value of the `gain'
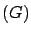 is given by the probability of each
event multiplied by the gain associated with each event:
is given by the probability of each
event multiplied by the gain associated with each event:
where the first factors of the
products on the right-hand side of the formula stand for probability,
the second for the amount of money.
It follows that
- Coherence requires the rational better to be indifferent
to the direction of the bet, i.e.
E
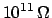 .
Applying this condition to
(
.
Applying this condition to
(![[*]](file:/usr/lib/latex2html/icons/crossref.png) )
we obtain (
)
we obtain (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).




Next: Are the beliefs in
Up: Appendix on probability and
Previous: Frequentists and combinatorial evaluation
Contents
Giulio D'Agostini
2003-05-15
![]() independently of
independently of
![]() and
and ![]() .
In fact,
.
In fact,
![]() is just the assessment of the probability
of
is just the assessment of the probability
of ![]() , under the condition that
, under the condition that ![]() is true. Then it cannot
depend on the probability of
is true. Then it cannot
depend on the probability of ![]() . It is easy to show with an example
that this point of view is rather natural, whilst that of considering
(
. It is easy to show with an example
that this point of view is rather natural, whilst that of considering
(![]() ) as a definition is artificial. Let us take
) as a definition is artificial. Let us take
![]() ) is a true theorem required by coherence.
It means that although one can speak of each of the three
probabilities independently of the others, once two of them have been
elicited, the third is constrained. It is interesting
to demonstrate the theorem to show that it has nothing to do with
the kind of heuristic derivation of Section
) is a true theorem required by coherence.
It means that although one can speak of each of the three
probabilities independently of the others, once two of them have been
elicited, the third is constrained. It is interesting
to demonstrate the theorem to show that it has nothing to do with
the kind of heuristic derivation of Section
![]() :
: