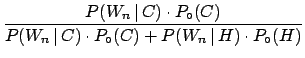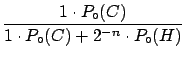,
and who
are trying to guess who
,
and who
are trying to guess who  is. Depending on the knowledge
they have about the friend, on the language spoken,
on the tone of voice, on the subject of conversation, etc.,
they will attribute some probability to several
possible persons. As the conversation goes on they begin
to consider some possible candidates for
is. Depending on the knowledge
they have about the friend, on the language spoken,
on the tone of voice, on the subject of conversation, etc.,
they will attribute some probability to several
possible persons. As the conversation goes on they begin
to consider some possible candidates for  , discarding others,
then hesitating perhaps only between a couple of possibilities,
until
the state of information
, discarding others,
then hesitating perhaps only between a couple of possibilities,
until
the state of information  . This experience
has happened to most of us, and it is not difficult to
recognize the Bayesian scheme:
. This experience
has happened to most of us, and it is not difficult to
recognize the Bayesian scheme:
We have put the initial state of information
 the probability will
be different from zero, without necessarily
favouring any particular person.
the probability will
be different from zero, without necessarily
favouring any particular person.
 meets an old friend
meets an old friend  accepts and
accepts and  who has to pay.
What is the probability that
who has to pay.
What is the probability that
The two hypotheses are: cheat (![]() ) and honest (
) and honest (![]() ).
).
![]() is low because
is low because ![]() is an ``old friend'',
but certainly not zero: let us assume
is an ``old friend'',
but certainly not zero: let us assume
![]() . To make the problem simpler let us make the approximation
that a cheat always wins (not very clever
. To make the problem simpler let us make the approximation
that a cheat always wins (not very clever![]() ):
):
![]() . The probability of winning if he is honest is, instead,
given by the rules of probability assuming that
the chance
of winning at each trial is
. The probability of winning if he is honest is, instead,
given by the rules of probability assuming that
the chance
of winning at each trial is ![]() (``why not?", we shall
come back to this point later):
(``why not?", we shall
come back to this point later):
![]() . The result
. The result
is shown in the following table.
|
|
|
|
| (%) | (%) | |
| 0 | 5.0 | 95.0 |
| 1 | 9.5 | 90.5 |
| 2 | 17.4 | 82.6 |
| 3 | 29.4 | 70.6 |
| 4 | 45.7 | 54.3 |
| 5 | 62.7 | 37.3 |
| 6 | 77.1 | 22.9 |
 increases. It is important to make two remarks.
increases. It is important to make two remarks.
- The answer is always probabilistic.
 can never reach
absolute certainty that
can never reach
absolute certainty that 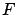 is a cheat,
unless he catches
is a cheat,
unless he catches 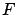 cheating, or
cheating, or 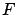 confesses to having cheated. This is coherent
with the fact that we are dealing with random events
and with the fact that any sequence of outcomes has the
same probability (although there is only one possibility over
confesses to having cheated. This is coherent
with the fact that we are dealing with random events
and with the fact that any sequence of outcomes has the
same probability (although there is only one possibility over
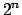 in which
in which 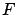 is always luckier). Making use
of
is always luckier). Making use
of
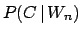 ,
,  can make a decision about the
next action to take:
can make a decision about the
next action to take:
- continue the game, with
probability
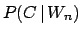 of losing with certainty the next time too;
of losing with certainty the next time too;
- refuse to play further, with probability
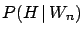 of offending the innocent friend.
of offending the innocent friend.
- continue the game, with
probability
- If
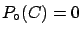 the final probability will
always remain zero: if
the final probability will
always remain zero: if  fully trusts
fully trusts 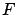 ,
then he has just to
record the occurrence of a rare event when
,
then he has just to
record the occurrence of a rare event when  becomes large.
becomes large.
To better follow the process of updating the probability when new experimental data become available, according to the Bayesian scheme
``the final probability of the present inference is the initial probability of the next one''.Let us call
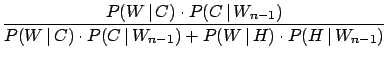 |
|||
| (3.22) | |||
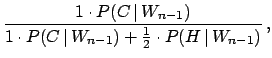 |
(3.23) |
where