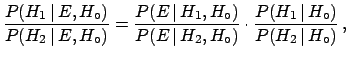Next: Choice of the initial
Up: Subjective probability and Bayes'
Previous: Bayesian statistics: learning by
Contents
Hypothesis test (discrete case)
Although in conventional statistics books this
argument is usually dealt with in one of the
later chapters, in the Bayesian
approach it is so natural that it is in fact
the first application, as we have seen in the
above examples. We summarize here the procedure:
- probabilities are attributed to the different
hypotheses using initial probabilities and
experimental data (via the likelihood);
- the person who makes the inference
-- or the ``user'' -- will make a decision
for which he is fully responsible.
If one needs to compare
two hypotheses, as in the example of the signal to noise
calculation, the ratio of the final probabilities
can be taken as a quantitative result of the test.
Let us rewrite the 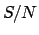 formula (
formula (![[*]](file:/usr/lib/latex2html/icons/crossref.png) )
in the most general case:
)
in the most general case:
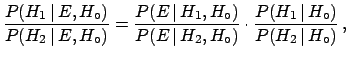 |
(3.24) |
where again we have reminded ourselves
of the existence of 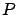 .
The ratio depends on the
product of two terms: the ratio of the priors
and the ratio of the likelihoods. When there is absolutely
no reason for choosing between the two hypotheses the
prior ratio is 1 and the decision depends only on the
other term, called the Bayes factor.
If one firmly believes in either hypothesis,
the Bayes
factor is of minor importance, unless it is zero or infinite
(i.e. one and only one of the likelihoods is vanishing).
Perhaps this is disappointing for those who expected
objective certainty from a probability theory, but
this is in the nature of things.
.
The ratio depends on the
product of two terms: the ratio of the priors
and the ratio of the likelihoods. When there is absolutely
no reason for choosing between the two hypotheses the
prior ratio is 1 and the decision depends only on the
other term, called the Bayes factor.
If one firmly believes in either hypothesis,
the Bayes
factor is of minor importance, unless it is zero or infinite
(i.e. one and only one of the likelihoods is vanishing).
Perhaps this is disappointing for those who expected
objective certainty from a probability theory, but
this is in the nature of things.




Next: Choice of the initial
Up: Subjective probability and Bayes'
Previous: Bayesian statistics: learning by
Contents
Giulio D'Agostini
2003-05-15