 is zero (
is zero ( have the same degree of belief
(and not only equal numerical
probability
have the same degree of belief
(and not only equal numerical
probability 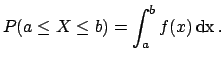 and then
and then
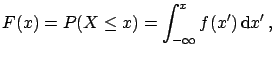 |
(4.25) |
 is zero (
is zero ( have the same degree of belief
(and not only equal numerical
probability
have the same degree of belief
(and not only equal numerical
probability 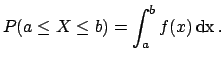 and then
and then
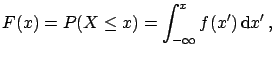 |
(4.25) |
After this short introduction, here is a list of definitions, properties and notations:
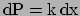 |
(4.26) |
or
| (4.27) |
E![$\displaystyle [X]$](img452.png) |
(4.28) | ||
E![$\displaystyle [g(X)]$](img454.png) |
(4.29) |
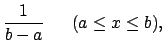 |
(4.30) | ||
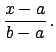 |
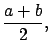 |
(4.31) |
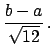 |
(4.32) | ||
| (4.33) |
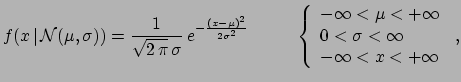 :
:
| (4.34) |
the particular normal distribution of mean 0 and standard
deviation 1, usually indicated by ![]() :
:
| (4.35) |
![]() :
:
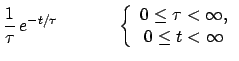 |
(4.36) | ||
| (4.37) |
| (4.38) |
| (4.39) | |||
| (4.40) |
If  (= ``number of counts during the time
(= ``number of counts during the time ![]() '') is
Poisson distributed then
'') is
Poisson distributed then ![]() (= ``interval of time to wait --
starting from any instant -- before the first count
is recorded'') is exponentially distributed:
(= ``interval of time to wait --
starting from any instant -- before the first count
is recorded'') is exponentially distributed:
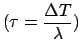 |
(4.41) | ||
| (4.42) |