Uncertainty in physics

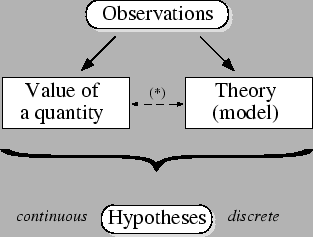
Figure: From observations to hypotheses. The link between value of a quantity and theory is a reminder that sometimes a physics quantity has meaning only within a given theory or model.

It is fairly well accepted among physicists that any conclusion which results from a measurement is affected by a certain degree of uncertainty. Let us remember briefly the reasons which prevent us from reaching certain statements. Figure 1.1 sketches the activity of physicists (or of any other scientist). From experimental data one wishes to determine the value of a given quantity, or to establish which theory describes the observed phenomena better. Although they are often seen as separate, both tasks may be viewed as two sides of the same process: going from observations to hypotheses. In fact, they can be stated in the following terms.

A:

Which values are (more) compatible with the definition of the measurand, under the condition that certain numbers have been observed on instruments (and subordinated to all the available knowledge about the instrument and the measurand)?

B:

Which theory is (more) compatible with the observed phenomena (and subordinated to the credibility of the theory, based also on aesthetics and simplicity arguments)?

The only difference between the two processes is that in the first the number of hypotheses is virtually infinite (the quantities are usually supposed to assume continuous values), while in the second it is discrete and usually small.

The reasons why it is impossible to reach the ideal condition of certain knowledge, i.e. only one of the many hypotheses is considered to be true and all the others false, may be summarized in the following, well-understood, scheme.

A:

As far as the determination of the value of a quantity is concerned, one says that ``uncertainty is due to measurement errors''.

B:

In the case of a theory, we can distinguish two subcases:

(B$_1$)

The law is probabilistic, i.e. the observations are not just a logical consequence of the theory. For example, tossing a regular coin, the two sequences of heads and tails

$${\tt hhhhhhhhhhhhhhhhhhhhhhhhh}$$

$${\tt hhttttthhhhthhtthhhththht}$$

have the same probability of being observed (as any other sequence). Hence, there is no way of reaching a firm conclusion about the regularity of the coin after an observed sequence of any particular length.^1.1

(B$_2$)

The law is deterministic. But this property is only valid in principle, as can easily be understood. In fact, in all cases the actual observations also depend on many other factors external to the theory, such as initial and boundary conditions, influence factors, experimental errors, etc. All unavoidable uncertainties on these factors mean that the link between theory and observables is of a probabilistic nature in this case too.