



Next: Counting measurements in the
Up: Uncertainty due to systematic
Previous: Measuring two quantities with
Contents
Let us use the result of the previous section to solve
another typical problem of measurements. Suppose that
after (or before, it doesn't matter) we have done the measurements
of 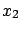 and
and 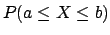 and we have the final result, summarized in
(
and we have the final result, summarized in
(![[*]](file:/usr/lib/latex2html/icons/crossref.png) ), we know the ``exact'' value of
), we know the ``exact'' value of 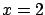 (for example we perform the measurement on a reference).
Let us call it
(for example we perform the measurement on a reference).
Let us call it
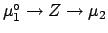 .
Will this information provide a better knowledge of
.
Will this information provide a better knowledge of 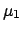 ?
In principle yes: the difference between
?
In principle yes: the difference between 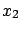 and
and
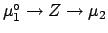 defines the systematic error
(the true value of the ``zero''
defines the systematic error
(the true value of the ``zero'' 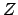 ). This error can
then be subtracted from
). This error can
then be subtracted from 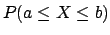 to get a corrected value.
Also the overall uncertainty of
to get a corrected value.
Also the overall uncertainty of 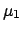 should change, intuitively
it ``should'' decrease, since we are adding new information.
But its value doesn't seem to be obvious, since the
logical link between
should change, intuitively
it ``should'' decrease, since we are adding new information.
But its value doesn't seem to be obvious, since the
logical link between
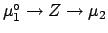 and
and 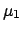 is
is
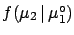 .
.
The problem can be solved exactly using the concept of conditional
probability density function
 [see (
[see (![[*]](file:/usr/lib/latex2html/icons/crossref.png) )-(
)-(![[*]](file:/usr/lib/latex2html/icons/crossref.png) )). We get
)). We get
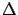 |
(5.83) |
The best value of 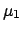 is shifted by an amount
is shifted by an amount 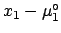 ,
with respect to the measured value
,
with respect to the measured value 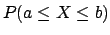 , which is
not exactly
, which is
not exactly
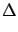 , as
was naï vely guessed,
and the uncertainty depends on
, as
was naï vely guessed,
and the uncertainty depends on 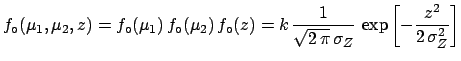 ,
, 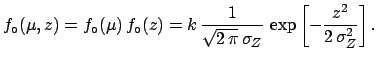 and
and 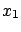 . It is easy to be convinced that the
exact result is more reasonable than the (suggested) first guess.
Let us rewrite
. It is easy to be convinced that the
exact result is more reasonable than the (suggested) first guess.
Let us rewrite 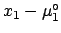 in two different ways:
in two different ways:




Next: Counting measurements in the
Up: Uncertainty due to systematic
Previous: Measuring two quantities with
Contents
Giulio D'Agostini
2003-05-15
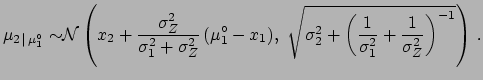 [see (
[see (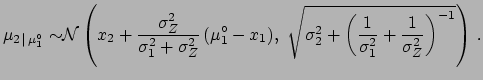 [see (
[see (![]() )-(
)-(![]() )). We get
)). We get
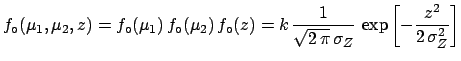 ,
, 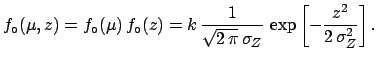 and
and 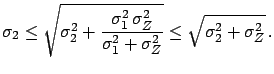 the correction is half of the measured difference between
the correction is half of the measured difference between
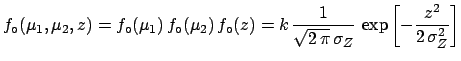 and the uncertainty of the
weighted average of the two offsets. Its value is smaller than
it would be with only one calibration and, obviously,
larger than that due to the sampling fluctuations alone:
and the uncertainty of the
weighted average of the two offsets. Its value is smaller than
it would be with only one calibration and, obviously,
larger than that due to the sampling fluctuations alone: