The idea of using (natural) logarithms of the odds
is quite old, going back, as far as I know,
to Charles Sanders Peirce [6].
He related them to what he called
feeling of belief (or intensity of belief),
that, according to him,
``should be as the logarithm
of the chance, this latter being the expression of the state
of facts which produces the belief'' [6], where by `chance'
he meant exactly probability ratios, i.e. the odds.
Peirce proposed his
''thermometer for the proper intensity of belief'' [6]
for several reasons.
- First because of
considerations that when the odds
go to zero or to infinity, then the intensity of belief on either
hypothesis goes to infinity;46
when ``an even chance is reached
[the feeling of believing] should completely vanish
and not incline either toward or away from the proposition.'' [6]
The logarithmic function is the simplest one to achieve the
desired feature. (Another interesting feature of the odds is
described in footnote 16.)
- Then because
(expressing the question in our terms),
if we started from a state of indifference (initial odds equal to 1),
each piece of evidence should produce odds equal
to its Bayes factor [our
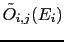 ]. The combined odds will be
the product of the individual odds
[Eq. 19].
But, mixing now Pierce's and our terminology,
when we combine several arguments (pieces of evidence),
they ``ought to produce a belief equal to the sum
of the intensities of belief which either would produce
separately''. [6] Then ``because we have seen that the chances
of independent concurrent arguments are to be multiplied together
to get the chance of their combination, and therefore
the quantities which best express the intensities
of belief should be
such that they are to be added when the chances
are multiplied...Now, the logarithm of the chance
is the only quantity which fulfills this condition''. [6]
]. The combined odds will be
the product of the individual odds
[Eq. 19].
But, mixing now Pierce's and our terminology,
when we combine several arguments (pieces of evidence),
they ``ought to produce a belief equal to the sum
of the intensities of belief which either would produce
separately''. [6] Then ``because we have seen that the chances
of independent concurrent arguments are to be multiplied together
to get the chance of their combination, and therefore
the quantities which best express the intensities
of belief should be
such that they are to be added when the chances
are multiplied...Now, the logarithm of the chance
is the only quantity which fulfills this condition''. [6]
- Finally, Peirce justifies his choice by the fact
that human perceptions go often as the logarithm of
the stimulus (think at subjective feeling of
sound and light - even `utility',
meant as the `value of money' is supposed
to grow logarithmically
with the amount of money):
``There is a general law of sensibility,
called Fechner's psychophysical law. It is that the intensity
of any sensation is proportional to the logarithm of the external
force which produces it.''[6]
(Table 1 provides a comparisons between the different
quantities involved, to show that the human sensitivity on probabilistic
judgement is indeed logarithmic, with a resolution about the first
decimal digit of the base 10 logarithms.)
As far as the logarithms in question, I have
done a short research on their use,
which, actually, lead me to discover Peirce's
Probability of Intuition [6]
and Good's Probability and the weighing of
Evidence [7].47As far as I understand, without pretension
of completeness or historical exactness:
- Peirce' `chances' are introduced as if they were our odds,
but are used if they were Bayes factors
(``the chances of
independent concurrent arguments are to be multiplied together
to get the chance of their combination'' [6]).
Then he takes the natural logarithm of these `chances',
to which he also associates an idea of weight of evidence
(``our belief ought to be proportional to the
weight of evidence, in the sense, that two arguments which are
entirely independent, neither weakening nor strengthening each other,
ought, when they concur, to produce a belief equal to the sum of the
intensities of belief which either would produce
separately'' [6]).
- According to Ref. [8]
the modern use of the logarithms of the
odds seem to go back to I.J. Good, who used
to call log-odds the natural logarithm
of the odds.48
- However, reading later Ref. [8] it is clear that
Good, following a suggestion of A.M. Turing,
proposes a decibel-like (db)
notation49,
giving proper names both to the logarithm of the
odds and to the logarithm of the Bayes factor:
- ``
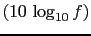 db ...
may be also described as the weight of
evidence or amount of information for
db ...
may be also described as the weight of
evidence or amount of information for 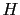 given
given 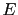 '' [7];
'' [7];
- ``
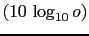 db may be called the plausibility
corresponding to odds
db may be called the plausibility
corresponding to odds 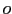 '' [7].
'' [7].
It follows then that
| ``Plausibility gained |
 |
weight of evidence''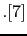 |
(36) |
- Decibel-like logarithms of the odds are used
since at least forty years with under the name
evidence. [23].
Personally, I think that
the decibel-like definition
is not very essential (decibels themselves
tend already to confuse normal people,
also because for some applications
the factor 10 is replaced by a factor 20).
Instead, as far as names are concerned:
- `plausibility' is difficult to defend, because
it is too similar to probability in everyday use,
and, as far as I understand, has decayed;
- `weight of evidence' seems to be a good choice,
for the reasons already well clear to Peirce.
- `evidence' in the sense of Ref. [23]
seems, instead, quite bad for a couple of reasons:
- First,
because `evidence'
has already too many meanings, including,
in the Bayesian literature, the denominator
of the r.h.s. of Eq. (3).
- Second, because this name is given to the logs of the odds
(including the initial ones), but not to those of the
Bayes factors to which no name is given. Therefore,
the name `evidence', as used in Ref. [23]
in this context, is not related to the evidence.
I have taken the liberty to use the expression `judgment
leaning'
first because it evokes the famous balance of Justice,
then because all other expressions I thought about have already
a specific meaning, and some of them even several
meanings.50It is clear, especially comparing
Eq. (36)
with Eq. (24),
that, besides the factor ten multiplying
the base ten logarithms and the notation,
I am quite in tune with Good.
I have also to admit I like Peirce'
`intensity of belief' to name the JL's,
although it is too similar to `degree of belief',
already widely used to mean something else.
So, in summary, these are the symbols and names used here:
-
JL
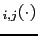
- is the
judgement leaning in favor
of hypothesis
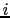 and against
and against 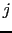 , with the conditions in parenthesis.
If we only consider
an hypothesis (
, with the conditions in parenthesis.
If we only consider
an hypothesis (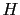 ) and its opposite
) and its opposite
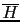 ,
that could be possibly related to the occurrence of the
event
,
that could be possibly related to the occurrence of the
event 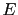 or its opposite
or its opposite
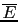 , also the notation
JL
, also the notation
JL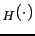 , or
JL
, or
JL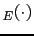 , will
be used (as in table 2 of Appendix I).
, will
be used (as in table 2 of Appendix I).
(Sometimes I have also tempted to call a JL `intensity
of belief' if it is clear from the contest that the expression
does not refer to a probability.)
-
 JL
JL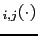
- , with the
same meaning of the subscript and of the argument, is the
variation of judgement leaning produced by
a piece of evidence and it is called here
weight of evidence, although it differs by a factor from
the analogous names used by
Peirce and Good51.
Giulio D'Agostini
2010-09-30