


Next: Conclusions
Up: Fits, and especially linear
Previous: From power law to
Systematic errors
Let us now consider the effect of systematic errors,
i.e. errors that acts the same way on all observations
of the sample, for example an uncertain offset in
the instrument scale, or an uncertain scale factor.
I do not want to give a complete treatment of the subjects,
but focus only on how our systematic effects
modify our graphical model,
and give some practical rules for the simple case of linear fits.
(For an introduction about systematic errors and their consistent
treatment within the Bayesian approach see Ref. [2].)
For each coordinate we can introduce the fictitious quantities
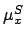 and
and 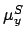 that take into account the
modification of
that take into account the
modification of 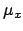 and
and 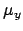 due to the systematic effect.
For example, if the systematic effects only acts as an offset,
i.e. we are uncertain about the
`true' zero of the instruments,
due to the systematic effect.
For example, if the systematic effects only acts as an offset,
i.e. we are uncertain about the
`true' zero of the instruments, 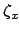 and
and 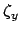 ,
we have
,
we have
where the true value of 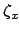 are
are 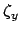 unknown (otherwise there would be no systematic errors).
We only know that their expected value is zero (otherwise
we need to apply a calibration constant to the measurements)
and we quantify our uncertainty with pdf's. For example,
we could model them with Gaussian distributions:
unknown (otherwise there would be no systematic errors).
We only know that their expected value is zero (otherwise
we need to apply a calibration constant to the measurements)
and we quantify our uncertainty with pdf's. For example,
we could model them with Gaussian distributions:
Anyway, for sake of generality, we leave the systematic
effects in the most general form, dependent on the uncertain
quantities
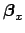 and
and
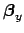 [to be clear:
in the case of solely offset systematics we have
[to be clear:
in the case of solely offset systematics we have
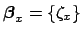
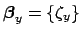 ].
The values of
].
The values of 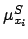 and
and 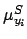 are modeled as follow
are modeled as follow
Figure 3
Figure 3:
Graphical model of Fig. 2
with the addition
of systematic errors on both axes.
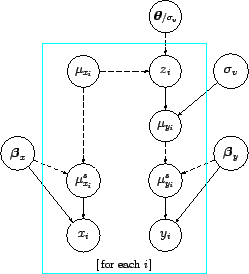 |
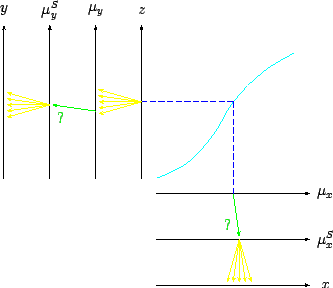
Figure 4:
A different visual representation
of the probabilistic model of Fig. 3.
 |
shows the graphical model containing the
new ingredients.
The links
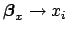 and
and
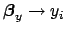 are to remember that
systematics could also effect the error functions.
An alternative visual picture of the
probabilistic model is shown in Fig. 4.
Note the different symbols to indicate the different uncertain
processes: the divergent arrows (in yellow, if you are reading
an electronic version of the paper) indicate that, given a value
of the `parent' variable, the `child' variable fluctuates on an event-by-event
basis; the green single arrow with the question mark indicate that,
given a value of the `parent', the child will always take a fixed value,
though we do not know which one.
are to remember that
systematics could also effect the error functions.
An alternative visual picture of the
probabilistic model is shown in Fig. 4.
Note the different symbols to indicate the different uncertain
processes: the divergent arrows (in yellow, if you are reading
an electronic version of the paper) indicate that, given a value
of the `parent' variable, the `child' variable fluctuates on an event-by-event
basis; the green single arrow with the question mark indicate that,
given a value of the `parent', the child will always take a fixed value,
though we do not know which one.
Obviously, the practical implementation of complicate systematic
effects in complicate fits can be quite challenging, but at least
the Bayesian network provides an overall picture of the model.
The simplest case is that of linear fit where only offset
and scale uncertainty are present, with uncertainty modeled
by a Gaussian distribution.
This means that the
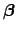 's and their uncertainty are as follows
(
's and their uncertainty are as follows
(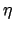 is the scale factor of uncertain value):
is the scale factor of uncertain value):
In this case we can get
an hint of how the uncertainty about 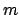 and
and 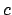 change without
doing the full calculation
following an heuristic approach, valid when
change without
doing the full calculation
following an heuristic approach, valid when
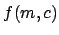 is approximately multivariate Gaussian and
the details of which can be found
in Ref. [16]. We obtain the following results,
in which
is approximately multivariate Gaussian and
the details of which can be found
in Ref. [16]. We obtain the following results,
in which
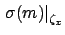 indicates the contribution
to the uncertainty about the slope
indicates the contribution
to the uncertainty about the slope 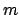 due to uncertainty
about
due to uncertainty
about 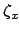 ,
,
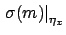 that due to the scale factor
that due to the scale factor 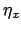 , and so
on7:
, and so
on7:
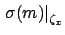 |
 |
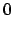 |
(82) |
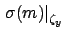 |
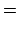 |
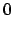 |
(83) |
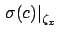 |
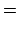 |
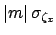 |
(84) |
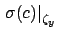 |
 |
 |
(85) |
| |
|
|
|
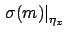 |
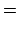 |
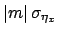 |
(86) |
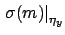 |
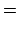 |
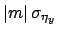 |
(87) |
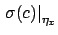 |
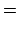 |
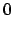 |
(88) |
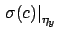 |
 |
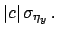 |
(89) |
All contributions are then added quadratically to the
so called `statistical' ones.



Next: Conclusions
Up: Fits, and especially linear
Previous: From power law to
Giulio D'Agostini
2005-11-21
![]() and
and ![]() that take into account the
modification of
that take into account the
modification of ![]() and
and ![]() due to the systematic effect.
For example, if the systematic effects only acts as an offset,
i.e. we are uncertain about the
`true' zero of the instruments,
due to the systematic effect.
For example, if the systematic effects only acts as an offset,
i.e. we are uncertain about the
`true' zero of the instruments, ![]() and
and ![]() ,
we have
,
we have
![]() 's and their uncertainty are as follows
(
's and their uncertainty are as follows
(![]() is the scale factor of uncertain value):
is the scale factor of uncertain value):