



Next: Deviazione standard della media
Up: Errori e incertezze di
Previous: Distribuzioni triangolari
Indice
Teorema del limite centrale
Ricordiamo brevemente quanto afferma il teorema del
limite centrale: la combinazione lineare di 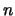 variabili
indipendenti (
variabili
indipendenti (
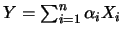 ) tende ad essere
distribuita
normalmente, con
) tende ad essere
distribuita
normalmente, con
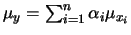 e
e
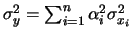 ,
quando
,
quando
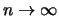 , se: a) le
, se: a) le 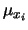 sono finite; b)
sono finite; b)
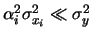 per ciascuna variabile
per ciascuna variabile 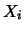 non distribuita normalmente. (Un altro modo di esprimere la seconda
condizione è che le
non distribuita normalmente. (Un altro modo di esprimere la seconda
condizione è che le
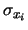 devono essere dello stesso ordine di grandezza
e solo variabili già distribuite normalmente possono fare eccezione;
non è invece necessario che siano dello stesso ordine di grandezza
anche le
devono essere dello stesso ordine di grandezza
e solo variabili già distribuite normalmente possono fare eccezione;
non è invece necessario che siano dello stesso ordine di grandezza
anche le 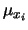 , in quanto eventuali costanti additive non
influenzano la distribuzione).
, in quanto eventuali costanti additive non
influenzano la distribuzione).
Si noti che il teorema non dice niente sul numero minimo
di componenti necessarie affinché esso sia valido.
Dipende dalle distribuzioni delle 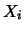 .
Ad esempio,
nel caso di variabili aventi la stessa distribuzione uniforme
è sufficiente
.
Ad esempio,
nel caso di variabili aventi la stessa distribuzione uniforme
è sufficiente 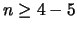 affinché l'approssimazione sia
ragionevole (è molto convincente
la figura 3, che
può essere reinterpretata, a parte un fattore
affinché l'approssimazione sia
ragionevole (è molto convincente
la figura 3, che
può essere reinterpretata, a parte un fattore 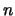 come
la distribuzione della media).
Se le distribuzionioni
hanno invece un massimo centrale sono sufficienti 2-3 componenti
(si noti
come 2 triangolari di uguale
come
la distribuzione della media).
Se le distribuzionioni
hanno invece un massimo centrale sono sufficienti 2-3 componenti
(si noti
come 2 triangolari di uguale 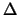 equivalgono a 4 uniformi).
Siccome nelle applicazioni alle incertezze di misura le
variabili di partenza sono
spesso ``quasi gaussiane'' la convergenza è generalmente molto
rapida49.
equivalgono a 4 uniformi).
Siccome nelle applicazioni alle incertezze di misura le
variabili di partenza sono
spesso ``quasi gaussiane'' la convergenza è generalmente molto
rapida49.




Next: Deviazione standard della media
Up: Errori e incertezze di
Previous: Distribuzioni triangolari
Indice
Giulio D'Agostini
2001-04-02
![]() .
Ad esempio,
nel caso di variabili aventi la stessa distribuzione uniforme
è sufficiente
.
Ad esempio,
nel caso di variabili aventi la stessa distribuzione uniforme
è sufficiente ![]() affinché l'approssimazione sia
ragionevole (è molto convincente
la figura 3, che
può essere reinterpretata, a parte un fattore
affinché l'approssimazione sia
ragionevole (è molto convincente
la figura 3, che
può essere reinterpretata, a parte un fattore ![]() come
la distribuzione della media).
Se le distribuzionioni
hanno invece un massimo centrale sono sufficienti 2-3 componenti
(si noti
come 2 triangolari di uguale
come
la distribuzione della media).
Se le distribuzionioni
hanno invece un massimo centrale sono sufficienti 2-3 componenti
(si noti
come 2 triangolari di uguale ![]() equivalgono a 4 uniformi).
Siccome nelle applicazioni alle incertezze di misura le
variabili di partenza sono
spesso ``quasi gaussiane'' la convergenza è generalmente molto
rapida49.
equivalgono a 4 uniformi).
Siccome nelle applicazioni alle incertezze di misura le
variabili di partenza sono
spesso ``quasi gaussiane'' la convergenza è generalmente molto
rapida49.