


Next: Probability of complete classes
Up: Rules of probability
Previous: Rules of probability
Probability of simple propositions
Let us start by recalling the basic rules of probability for propositions or hypotheses.
Let 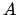 and
and 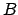 be propositions,
which can take on only two values, for example, true or false.
The notation
be propositions,
which can take on only two values, for example, true or false.
The notation 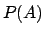 stands for the probability that
stands for the probability that 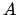 is true.
The elementary rules of probability for simple propositions are
is true.
The elementary rules of probability for simple propositions are
where 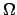 means tautology (a proposition that is
certainly true).
The construct
means tautology (a proposition that is
certainly true).
The construct 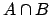 is true only when both
is true only when both 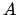 and
and 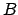 are true (logical AND),
while
are true (logical AND),
while 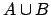 is true when at least one of the
two propositions is true (logical OR).
is true when at least one of the
two propositions is true (logical OR). 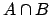 is also
written simply as `
is also
written simply as `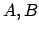 ' or
' or 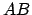 , and is also called a logical product,
while
, and is also called a logical product,
while 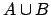 is also called a logical sum.
is also called a logical sum.
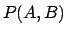 is called the joint probability of
is called the joint probability of 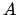 and
and 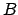 .
.
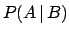 is the probability of
is the probability of 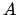 under that condition that
under that condition that 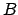 is true. We often read it
simply as ``the probability of A, given
is true. We often read it
simply as ``the probability of A, given 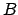 .'' .
.'' .
Equation (4) shows that the joint probability of
two events can be decomposed into conditional probabilities
in different two ways.
Either of these ways is called the product rule.
If the status of 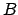 does not change the probability
of
does not change the probability
of 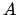 , and the other way around, then
, and the other way around, then
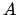 and
and 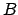 are said to be independent, probabilistically
independent to be precise. In that case,
are said to be independent, probabilistically
independent to be precise. In that case,
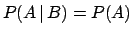 , and
, and
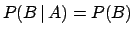 , which, when inserted in Eq. (4), yields
, which, when inserted in Eq. (4), yields
Equations (1)-(4) logically lead to
other rules which form the body of probability theory.
For example,
indicating the negation (or opposite)
of 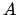 with
with 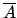 , clearly
, clearly
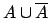 is a tautology (
is a tautology (
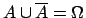 ),
and
),
and
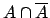 is a contradiction
(
is a contradiction
(
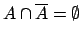 ).
The symbol
).
The symbol 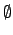 stands for contradiction
(a proposition that is certainly false).
Hence, we obtain from Eqs. (2) and (3)
stands for contradiction
(a proposition that is certainly false).
Hence, we obtain from Eqs. (2) and (3)
which says that proposition 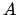 is either true or not true.
is either true or not true.



Next: Probability of complete classes
Up: Rules of probability
Previous: Rules of probability
Giulio D'Agostini
2003-05-13
![]() and
and ![]() be propositions,
which can take on only two values, for example, true or false.
The notation
be propositions,
which can take on only two values, for example, true or false.
The notation ![]() stands for the probability that
stands for the probability that ![]() is true.
The elementary rules of probability for simple propositions are
is true.
The elementary rules of probability for simple propositions are
![]() does not change the probability
of
does not change the probability
of ![]() , and the other way around, then
, and the other way around, then
![]() and
and ![]() are said to be independent, probabilistically
independent to be precise. In that case,
are said to be independent, probabilistically
independent to be precise. In that case,
![]() , and
, and
![]() , which, when inserted in Eq. (4), yields
, which, when inserted in Eq. (4), yields