Probability rules for uncertain variables

In analyzing the data from physics experiments, we need to deal with measurement that are discrete or continuous in nature. Our aim is to make inferences about the models that we believe appropriately describe the physical situation, and/or, within a given model, to determine the values of relevant physics quantities. Thus, we need the probability rules that apply to uncertain variables, whether they are discrete or continuous. The rules for complete classes described in the preceding section clearly apply directly to discrete variables. With only slight changes, the same rules also apply to continuous variables because they may be thought of as a limit of discrete variables, as interval between possible discrete values goes to zero.

For a discrete variable $x$, the expression $p(x)$, which is called a probability function, has the interpretation in terms of the probability of the proposition $P(A)$, where $A$ is true when the value of the variable is equal to $x$. In the case of continuous variables, we use the same notation, but with the meaning of a probability density function (pdf). So $p(x) \, dx$, in terms of a proposition, is the probability $P(A)$, where $A$ is true when the value of the variable lies in the range of $x$ to $x + dx$. In general, the meaning is clear from the context; otherwise it should be stated. Probabilities involving more than one variable, like $p(x,y)$, have the meaning of the probability of a logical product; they are usually called joint probabilities.

Table 1 summarizes useful formulae for discrete and continuous variables. The interpretation and use of these relations in Bayesian inference will be illustrated in the following sections.

Table: Some definitions and properties of probability functions for values of a discrete variable $x_i$ and probability density functions for continuous variables $x$. All summations and integrals are understood to extend over the full range of possibilities of the variable. Note that the expectation of the variable is also called expected value (sometimes expectation value), average and mean. The square root of the variance is the standard deviation $\sigma$.

	discrete variables	continuous variables
probability	$P(X=x_i) = p(x_i)$	$\,\mbox{d}P_{[x\le X \le x+\,\mbox{d}x]}= p(x) \,\mbox{d}x$
normalization$^\dag$	$\sum_i p(x_i) = 1$	$\int\!p(x)\,\mbox{d}x = 1$
expectation of $f(X)$	$\mbox{E}[f(X)] = \sum_i f(x_i) \, p(x_i)$	$\mbox{E}[f(X)] = \int\!f(x) \, p(x)\,\mbox{d}x$
expected value	$\mbox{E}(X) = \sum_i x_i \, p(x_i)$	$\mbox{E}(X) = \int\!x \, p(x)\,\mbox{d}x$
moment of order $r$	$\mbox{M}_r(X) = \sum_i x_i^r \, p(x_i)$	$\mbox{M}_r(X) = \int\!x^r \, p(x)\,\mbox{d}x$
variance	$\sigma^2 = \sum_i [x_i-\mbox{E}(X)]^2 \, p(x_i)$	$\sigma^2 = \int [x-\mbox{E}(X)]^2 \, p(x)\,\mbox{d}x$
product rule	$p(x_i,y_j) = p(x_i\,\vert\,y_j)\,p(y_j)$	$p(x,y) = p(x\,\vert\,y)\,p(y)$
independence	$p(x_i,y_j) = p(x_i)\,p(y_j)$	$p(x,y) = p(x)\,p(y)$
marginalization	$\sum_jp(x_i,y_j) = p(x_i)$	$\int\!p(x,y)\,\mbox{d}y = p(x)$
decomposition	$p(x_i) = \sum_jp(x_i\,\vert y_j)\,p(y_j)$	$p(x) = \int\!p(x\,\vert\,y)\, p(y)\,\mbox{d}y$
Bayes' theorem	$p(x_j\,\vert\,y_i) = \frac{\textstyle p(y_i\,\vert\,x_j)\,p(x_j)} {\textstyle \sum_jp(y_i\,\vert\,x_j)\,p(x_j)}$	$p(x\,\vert\,y) = \frac{\textstyle p(y\,\vert\,x)\,p(x)} {\textstyle \int p(y\,\vert\,x)\,p(x)\,\mbox{d}x}$
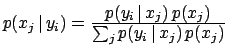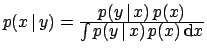likelihood	${\cal L}(x_j\,;\,y_i) = p(y_i\,\vert\,x_j)$	${\cal L}(x\,;\,y) = p(y\,\vert\,x)$
$^\dag$A function $p(x)$ such that $\sum_i p(x_i) = \infty$, or $\int\!p(x)\,\mbox{d}x = \infty$, is called improper. Improper
functions are often used to describe relative beliefs about the possible values of a variable.